
2. 列题纲使要点条理化,有序化,统筹安排布局。
1. 首先要认真审题。读懂题目所给信息,初步确定要点内容,并可用序号标出以免遗忘。
1.3.1利用导数判断函数的单调性
|
学习目标: 1.正确理解利用导数判断函数的单调性的原理; 2.掌握利用导数判断函数单调性的方法  学习重点难点: 利用导数判断函数单调性  . .自主学习 一、知识再现: 1. 函数的单调性. 对于任意的两个数x1,x2∈I,且当x1<x2时, 都有f(x1)<f(x2),那么函数f(x)就是区间I上的增函数. 对于任意的两个 数x1,x2∈I,且当x1<x2时,都有f(x1)>f(x2),那么函数f(x)就是区间 I上的减函数. 2. 导数的概念及其四则运算 二、新课探究: 1、定义:一般地,设函数y=f(x) 在某个区间内有导数,如果在 这个区间内   0,那么函数y=f(x) 在为这个区间内的增函数;如果在 0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内   0,那么函数y=f(x) 在为这个区间内的减函数 0,那么函数y=f(x) 在为这个区间内的减函数  2、用导数求函数单调区间的步骤: ①求函数f(x)的导数f′(x). ②令f′(x)  0解不等式,得x的范围就是递增区间. 0解不等式,得x的范围就是递增区间.③令f′(x)  0解不等式,得x的范围,就是递减区间. 0解不等式,得x的范围,就是递减区间.3、例题解析: 例1确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函 数. 解:f′(x)=(x2-2x+4)′=2x-2. 令2x-2>0,解得x>1. ∴当x∈(1,+∞)时,f′(x)>0,f(x)是增函数. 令2x-2<0,解得x<1. ∴当x∈(-∞,1)时,f′(x)<0,f(x)是减函数. 例2确定函数f(x)=2x3-6x2+7在哪个区间内是增函数,哪个区间内是减 函数. 解:f′(x)=(2x3-6x2+7)′=6x2-12x 令6x2-12x>0,解得x>2或x<0 ∴当x∈(-∞,0)时,f′(x)>0,f(x)是增函数. 当x∈(2,+∞)时,f′(x)>0,f(x)是增函数. 令6x2-12x<0,解得0<x<2. ∴当x∈(0,2)时,f′(x)<0,f(x)是减函数. 例3证明函数f(x)=  在(0,+∞)上是减函数. 在(0,+∞)上是减函数.证法一:(用以前学的方法证)任取两个数x1,x2∈(0,+∞)设x1<x2. f(x1)-f(x2)=  ∵x1>0,x2>0,∴x1x2>0 ∵x1>0,x2>0,∴x1x2>0∵x1<x2,∴x2-x1>0, ∴  >0 >0∴f(x1)-f(x2)>0,即f(x1)>f(x2) ∴f(x)=  在(0,+∞)上是减函数. 在(0,+∞)上是减函数.证法二:(用导数方法证) ∵f′(x)=(  )′=(-1)·x-2=- )′=(-1)·x-2=- ,x>0, ,x>0,∴x2>0,∴-  <0.
∴f′(x)<0,∴f(x)= <0.
∴f′(x)<0,∴f(x)=  在(0,+∞)上是减函数. 在(0,+∞)上是减函数.例4求函数y=x2(1-x)3的单调区间. 解:y′=[x2(1-x)3]′=2x(1-x)3+x2·3(1-x)2·(-1) =x(1-x)2[2(1-x)-3x]=x(1-x)2·(2-5x) 令x(1-x)2(2-5x)>0,解得0<x<  . . ∴y=x2(1-x)3的单调增区间 是(0,  ) 令x(1-x)2(2-5x)<0,解得x<0或x> ) 令x(1-x)2(2-5x)<0,解得x<0或x> 且x≠1. 且x≠1.∵  为拐点,∴y=x2(1-x)3的单调减区间是(-∞,0),( 为拐点,∴y=x2(1-x)3的单调减区间是(-∞,0),( ,+∞) ,+∞)例5.求  的单调递增区间 的单调递增区间解:由函数的定义域可知,  即 即 又   所以  令  ,得 ,得  或 或 综上所述,  的单调递增区间为(0,1) 的单调递增区间为(0,1)课堂巩固: 1.函数  的单调递增区间是( ) 的单调递增区间是( )A  B B  C C  D D  2.已知函数  ,则它的单调递减区间是( ) ,则它的单调递减区间是( )A.  B. B. C. C.  D. D. 及 及 3. 函数   的单调递增区间是__________________. 的单调递增区间是__________________.4.当  时,
时, 在 在 上是减函数. 上是减函数.归纳反思: 合作探究: 1.求函数  的单调区间 的单调区间2.已知函数  的图象过点 的图象过点 ,且在点 ,且在点 处的切线方程为 处的切线方程为 。 。(1)求函数  的解析式;(2)求函数 的解析式;(2)求函数 的单调区间。 的单调区间。 |
教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 教师备课 学习笔记 |
36. [浙江省五校2009届高三第一次联考数学(理科)试题卷第20题](本小题满分15分)
已知函数 .
.
(Ⅰ)若函数 与
与 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数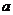 的值并求点P的坐标;
的值并求点P的坐标;
(Ⅱ)若函数 与
与 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求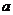 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过线段MN的中点作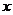 轴的垂线分别与
轴的垂线分别与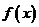 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作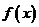 的切线
的切线 ,以T为切点作
,以T为切点作 的切线
的切线 .是否存在实数
.是否存在实数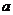 使得
使得

 ,如果存在,求出
,如果存在,求出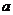 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
35、[广东省南海中学2009届高三12月统测数学(理科)试卷第19题] (14分)
已知函数 ,且对于任意实数
,且对于任意实数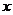 ,恒有
,恒有 。
。
(1)求函数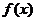 的解析式;
的解析式;
(2)已知函数 在区间
在区间 上单调,求实数
上单调,求实数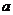 的取值范围;
的取值范围;
(3)函数 有几个零点?
有几个零点?
34. [江苏省连云港东海高复中心数学迎二模练习(1)第19题]
已知函数 .
.
(1)当a=1时,证明函数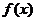 只有一个零点;
只有一个零点;
(2)若函数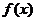 在区间(1,+∞)上是减函数,求实数a的取值范围
在区间(1,+∞)上是减函数,求实数a的取值范围
33.[福建省福州八中2008-2009学年度高三第四次质量检查数学(理科)第20题](本小题满分12分)
已知函数
(Ⅰ)若函数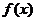 在
在 上为增函数,求正实数
上为增函数,求正实数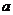 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论
时,讨论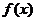 在
在 的单调性.
的单调性.
32、[湛江二十一中2007-2008学年度高三数(理)模拟测试(5)第19题] (本小题满分13分)
设函数
(1)求函数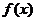 的单调区间
的单调区间
(2)当 时,求函数
时,求函数 在区间
在区间 上的最小值。
上的最小值。
31、[广东省南海中学2009届高三12月统测数学(理科)试卷第16题] (12分)
已知函数 ,
,
(1)求函数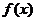 的单调区间;
的单调区间;
(2)若
 为大于0的常数),求
为大于0的常数),求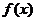 的最大值.
的最大值.
30.[福建省福州八中2008-2009学年度高三第四次质量检查数学(理科)第5题]
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
|
f(1)=-2 |
f(1.5)=0.625 |
f(1.25)=-0.984 |
|
f(1.375)=-0.260 |
f(1.4375)=0.162 |
f(1.40625)=-0.054 |
那么方程 的一个近似根(精确到0.1)为 ( )
的一个近似根(精确到0.1)为 ( )
A. 1.5 B. 1.4 C. 1.3 D. 1.2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com