
3. -Go and ask her come .
-OK.
A.what time would she like to B.at what time she’d like to
C.when would she like to D.when she likes to
2. -I rang you at about nine, but there was no reply.
-Oh, that was probably I was seeing the doctor.
A.why B.when C.what D.that
1. She looks sad. Could you please tell me ____ that prevents her from being as happy as before?
A. what it is B. it is what C. how it is D. it is how
2.设函数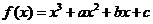 的图象如图所示,且与
的图象如图所示,且与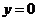 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为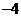 ,(1)求
,(1)求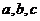 的值;(2)求函数的递减区间.
的值;(2)求函数的递减区间.
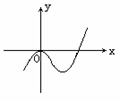
1.设f(x)=x3+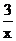 ,求函数f(x)的单调区间及其极值.
,求函数f(x)的单调区间及其极值.
4. 若函数y=x3+ax2+bx+27在x=-1时有极大值,在x=3时有极小值,则a=___________,b=___________.
归纳反思:
课后探究:
3.函数y=-x3+48x-3的极大值为___________;极小值为_________
2.y=ln2x+2lnx+2的极小值为( ) A.e-1 B.0 C.-1 D.1
1.函数y=x3-3x的极大值为m,极小值为n,则m+n为( )
A.0 B.1 C.2 D.4
1.3.2利用导数研究函数的极值
(第一课时)
|
学习目标: 掌握求可导函数的极值的步骤  学习重点难点: 掌握求可导函数的极值的步骤  自主学习 一、知识回顾: 1. 函数的导数与函数的单调性的关系:设函数y=f(x) 在某个区间内有导数,如果在这个区间内  >0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内 >0,那么函数y=f(x) 在为这个区间内的增函数;如果在这个区间内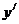 <0,那么函数y=f(x) 在为这个区间内的减函数 <0,那么函数y=f(x) 在为这个区间内的减函数  2.用导数求函数单调区间的步骤:①求函数f(x)的导数f′(x). ②令f′(x)>0解不等式,得x的范围就是递增区间.③令f′(x)<0解不等式,得x的范围,就是递减区间  二、新课探究 1.极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点  2.极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0).就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点  3.极大值与极小值统称为极值  在定义中,取得极值的点称为极值点,极值点是自变量的值,极值指的是函数值  请注意以下几点: 请注意以下几点:(ⅰ)极值是一个局部概念  由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小 由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小 并不意味着它在函数的整个的定义域内最大或最小 并不意味着它在函数的整个的定义域内最大或最小 (ⅱ)函数的极值不是唯一的  即一个函数在某区间上或定义域内极大值或极小值可以不止一个 即一个函数在某区间上或定义域内极大值或极小值可以不止一个 (ⅲ)极大值与极小值之间无确定的大小关系  即一个函数的极大值未必大于极小值,如下图所示, 即一个函数的极大值未必大于极小值,如下图所示,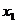 是极大值点, 是极大值点,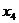 是极小值点,而 是极小值点,而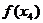 > >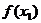  (ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点  而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点 而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点 4. 判别f(x0)是极大、极小值的方法: 若 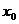 满足 满足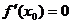 ,且在 ,且在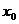 的两侧 的两侧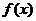 的导数异号,则 的导数异号,则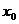 是 是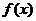 的极值点, 的极值点,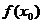 是极值,并且如果 是极值,并且如果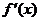 在 在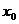 两侧满足“左正右负”,则 两侧满足“左正右负”,则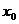 是 是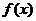 的极大值点, 的极大值点,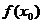 是极大值;如果 是极大值;如果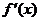 在 在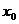 两侧满足“左负右正”,则 两侧满足“左负右正”,则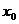 是 是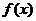 的极小值点, 的极小值点,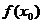 是极小值 是极小值 5. 求可导函数f(x)的极值的步骤: (1)确定函数的定义区间,求导数f′(x)  (2)求方程f′(x)=0的根  (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值  三、例题解析: 例1求y= 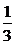 x3-4x+4的极值 x3-4x+4的极值 解:y′=( 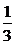 x3-4x+4)′=x2-4=(x+2)(x-2) x3-4x+4)′=x2-4=(x+2)(x-2)
 令y′=0,解得 令y′=0,解得x1=-2,x2=2  当x变化时,y′,y的变化情况如下表 当x变化时,y′,y的变化情况如下表
值且y极小值=- 例2求y=(x2-1)3+1的极值 解:y=6x(x2-1)2=6x(x+1)2(x-1)2令y′=0解得x1=-1,x2=0,x3=1 当x变化时,y′,y的变化情况如下表
∴当x=0时,y有极小值且y极小值=0
求极值的具体步骤:第一,求导数f′(x).第二,令f′(x)=0求方程的根,第三,列表,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值,如果左右都是正,或者左右都是负,那么f(x)在这根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否 是极值点 课堂巩固: 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |