
12.(2006年上海春)设函数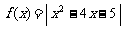 .
.
(1)在区间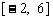 上画出函数
上画出函数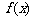 的图像;
的图像;
(2)设集合
 ,
,
试判断集合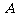 和
和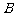 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当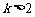 时,求证:在区间
时,求证:在区间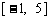 上,
上,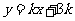 的图像位于函数
的图像位于函数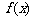 图像的上方.
图像的上方.
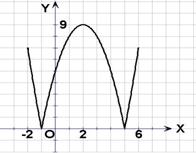
解:(1)如图所示:
(2)方程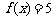 的解分别是
的解分别是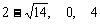 和
和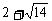 ,由于
,由于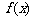 在
在 和
和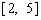 上单调递减,在
上单调递减,在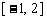 和
和 上单调递增,因此
上单调递增,因此
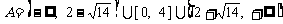 .
.
由于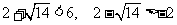 ,∴
,∴ .
.
(3)[解法一] 当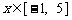 时,
时,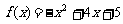 .
.
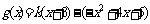
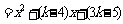
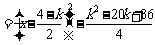 ,
,
 ,∴
,∴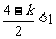 ,又
,又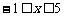 ,
,
① 当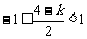 ,即
,即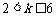 时,取
时,取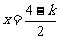 ,
,
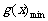
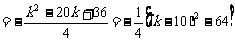 .
.
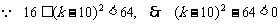 , 则
, 则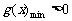 .
.
② 当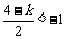 ,即
,即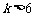 时,取
时,取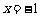 ,
, 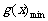 =
=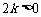 .
.
由 ①、②可知,当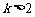 时,
时,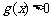 ,
,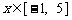 .
.
因此,在区间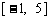 上,
上,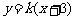 的图像位于函数
的图像位于函数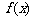 图像的上方.
图像的上方.
[解法二] 当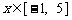 时,
时,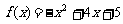 .
.
由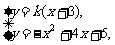 得
得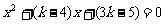 ,
,
令 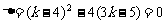 ,解得
,解得
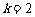 或
或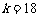 ,
,
在区间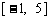 上,当
上,当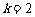 时,
时,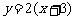 的图像与函数
的图像与函数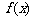 的图像只交于一点
的图像只交于一点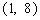 ;
当
;
当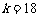 时,
时,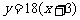 的图像与函数
的图像与函数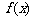 的图像没有交点.
的图像没有交点.
如图可知,由于直线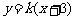 过点
过点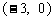 ,当
,当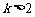 时,直线
时,直线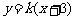 是由直线
是由直线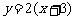 绕点
绕点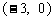 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间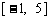 上,
上,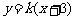 的图像位于函数
的图像位于函数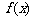 图像的上方.
图像的上方.
第三节 函数的奇偶性和周期性
自主学习
11.(2007湖北文)设二次函数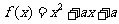 ,方程
,方程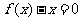 的两根
的两根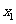 和
和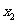 满足
满足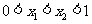 .
.
(1)求实数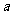 的取值范围;
的取值范围;
(2)试比较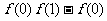 与
与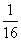 的大小,并说明理由.
的大小,并说明理由.
[解析](1)令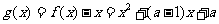 ,
,
则由题意可得
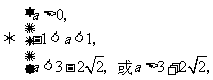
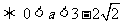 .
.
故所求实数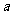 的取值范围是
的取值范围是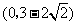 .
.
(2)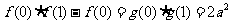 ,令
,令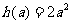 .
.
 当
当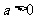 时,
时,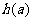 单调增加,
单调增加,
∴当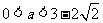 时,
时,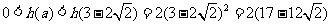
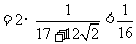 ,即
,即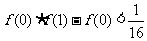 .
.
10.设f(x)、g(x)都是单调函数,有如下四个命题:
①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增;
②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增;
③若f(x)单调递减,g(x)单调递增,则f(x)-g(x)单调递减;
④若f(x)单调递减,g(x)单调递减,则f(x)-g(x)单调递减.
其中,正确的命题是 ② ③ .
三 解答题
9. 如果函数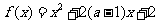 在区间
在区间 上是减函数,那么实数a的取值范围是
上是减函数,那么实数a的取值范围是 .
.
8.函数y=loga(2-ax)在[0,1]上是减函数,则a的取值范围是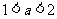 .
.
7.(2006年湖北省荆州市高中毕业班质量检查题)函数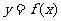 的图象与
的图象与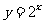 的图象关于直线
的图象关于直线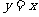 对称,则函数
对称,则函数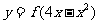 的递增区间是
的递增区间是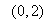 .
.
6. (2009山东文)已知定义在R上的奇函数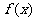 ,满足
,满足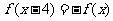 ,且在区间[0,2]上是增函数,则 ( D
).
,且在区间[0,2]上是增函数,则 ( D
).
A.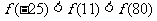 B.
B. 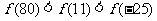
C. 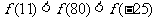 D.
D.
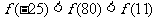
二 填空题
5.(2009浙江文)若函数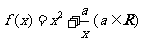 ,则下列结论正确的是(
C )
,则下列结论正确的是(
C )
A.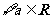 ,
,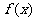 在
在 上是增函数21世纪教育网
上是增函数21世纪教育网
B.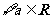 ,
,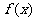 在
在 上是减函数
上是减函数
C.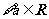 ,
,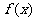 是偶函数
是偶函数
D.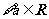 ,
,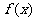 是奇函数
是奇函数
4. (2009广东文)函数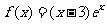 的单调递增区间是 ( D )
的单调递增区间是 ( D )
A.  B. (0,3) C. (1,4) D.
B. (0,3) C. (1,4) D. 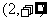 21世纪教育网
21世纪教育网
3.(2006年天津卷)已知函数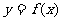 的图象与函数
的图象与函数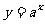 (
( 且
且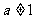 )的图象关于直线
)的图象关于直线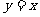 对称,记
对称,记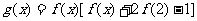 .若
.若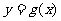 在区间
在区间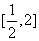 上是增函数,则实数
上是增函数,则实数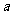 的取值范围是( D )
的取值范围是( D )
A.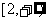 B.
B.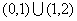 C.
C.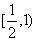 D.
D.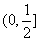
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com