
5.若α=-216°,l=7π,则r= (其中扇形的圆心角为α,弧长为l,半径为r).
4.圆的半径变为原来的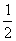 ,而弧长不变,则该弧所对的圆心角是原来
,而弧长不变,则该弧所对的圆心角是原来
的 倍.
3.一个半径为R的扇形,它的周长是4R,则这个扇形所含弓形的面积是( )

2.时钟经过一小时,时针转过了( )
A. 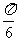 rad
B.-
rad
B.-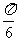 rad
C.
rad
C. 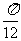 rad D.-
rad D.-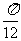 rad
rad
1.圆的半径变为原来的2倍,而弧长也增加到原来的2倍,则( )
A.扇形的面积不变 B.扇形的圆心角不变
C.扇形的面积增大到原来的2倍 D.扇形的圆心角增大到原来的2倍
例1.求图中公路弯道处弧AB的长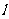 (精确到1m)图中长度单位为:m
(精确到1m)图中长度单位为:m
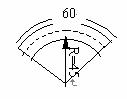 解: ∵
解: ∵ 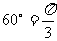
∴ 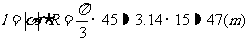
例2.已知扇形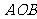 的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积
的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积
解:设扇形的半径为r,弧长为 ,则有
,则有
∴ 扇形的面积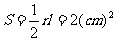
例3 计算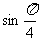 和
和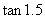
解:∵ 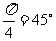 ∴
∴ 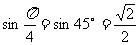
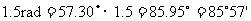
∴ 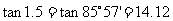
例4 将下列各角化成0到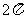 的角加上
的角加上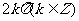 的形式
的形式
⑴ 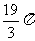 ⑵
⑵ 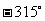
解: 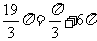

例5 直径为20cm的圆中,求下列各圆心所对的弧长 ⑴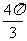 ⑵
⑵ 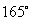
解: 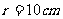 ⑴
⑴ 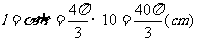
⑵ 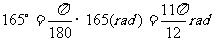 ∴
∴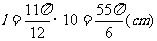
例6 已知扇形周长为10cm,面积为6cm2,求扇形中心角的弧度数.
解:设扇形中心角的弧度数为α(0<α<2π),弧长为l,半径为r,
由题意: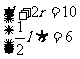

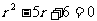
∴ 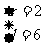 或
或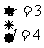 ∴
∴  =3 或
=3 或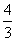
2.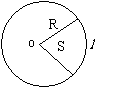 扇形面积公式
扇形面积公式
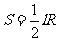 其中
其中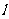 是扇形弧长,
是扇形弧长,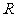 是圆的半径
是圆的半径
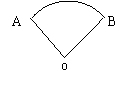
证:如图:圆心角为1rad的扇形面积为: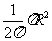
弧长为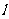 的扇形圆心角为
的扇形圆心角为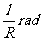
∴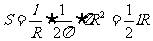
比较这与扇形面积公式 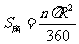 要简单
要简单
1.弧长公式: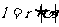
由公式: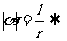
 比公式
比公式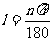 简单
简单
弧长等于弧所对的圆心角(的弧度数)的绝对值与半径的积
5.初中学过的弧长公式、扇形面积公式: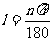 ;
;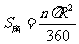
4.应确立如下的概念:角的概念推广之后,无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系
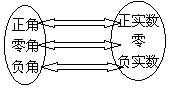
任意角的集合 实数集R
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com