6．(2010年江苏四市教学情况调查)根据下面一段文字，概括出“3G手机”的主要特点。(不超过15个字)

3G是英文3rdGaneration的缩写，指第三代移动通信技术。相对第一代模拟制式手机(1G)和第二代GSM、CDMA等数字手机(2G)，第三代手机优于前两代手机的具体表现就是手机联网的速率。现在移动GPRS一般最快也就是10kb/s，联通的CDMAlx也只有30kb/s左右，而3G时代可以让你的手机有如家庭宽带一样的网速。比如WCDMA的理论最小值是384kb/s，静止状态可达2Mkb/s。速率提上去了，3G手机就能够处理图像、音乐、视频流等多种媒体形式，提供包括网页浏览、电话会议、电子商务等多种信息服务。其标志性功能就是支持视频电话。目前，日本移动通讯巨人NTTDoCoMo已开通全球第一个3G服务，我国也已向中国移动、中国电信和中国联通发放3张3G牌照，亚洲成为全球3G发展最快的地区。

________________________________________________________________________

[解析]　第一点，要注意“速率”这个词；第二点概括“提供包括网页浏览、电话会议、电子商务等多种信息服务”时，不要写成具体的“网页浏览、电话会议、电子商务”或写“支持视频电话”等。

[答案]　联网速率快，提供服务多。

5．扩展下面的语句，使其生动、具体。(70个字左右)

琴声吸引了许多路人驻足倾听

________________________________________________________________________

________________________________________________________________________

[解析]　要使此句具体生动，就要展开联想和想像，对琴声如何吸引人进行一番描写和渲染。

[答案]　优美的《梁山伯和祝英台》小提瑟协奏曲，轻轻地飘出小白楼的窗户，穿过蒙蒙细雨，洒落在林间的小路上。许多行人情不自禁地停下了脚步，听得如痴如醉。

4．请拟一条以“公民义务献血”为内容的公益广告词。

要求：主题鲜明，感情真挚，构思新颖，语言简明。(在10-20个字之间)

________________________________________________________________________

[解析]　注意主题鲜明，构思新颖，要符合公益广告的要求。

[答案]　献出一滴热血，献上一片爱心。

3．根据以下规定的情境，以“免疫力”为中心，分别扩展成一段话。(每段40个字左右)

情境一：身体健康方面

________________________________________________________________________

________________________________________________________________________

情境二：社会影响方面

________________________________________________________________________

________________________________________________________________________

[解析]　本题考查扩写语句的能力，能力层级为D级。解答本题，一要明“情境”，二要显“中心”，三要合“字数”。写出来的答案要显示出二者之间的差别，前者从“身体健康方面”说，后者从“社会影响方向”说，换言之，前者从身体“免疫力”方面扩写，后者从比喻意义方面表现“免疫力”。

[答案]　情境一：只有不断提高身体免疫力，才能有强壮的身体，才能保持良好的状态，进而才能学习、工作。

情境二：只有不断提高社会免疫力，才能有坚定的信念，才能保持清醒的头脑，才能留住自我而不随波逐流。

2．扩展下面一句话，使内容更加具体、生动、形象。(50个字左右)

踏春归来，襟袖间还飘逸着春天的气息。

扩句：________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

[答案]　示例一：沐浴着明媚的阳光，怀着对春姑娘的深深眷恋，我挥挥衣袖，告别了青山绿水，衣袖间还沾着花间露水，嗅一下，还能闻到花的芳香；裙角间还残留着小草的新绿，散发着泥土的清香。

示例二：结伴去郊外踏青，春风轻轻地吹动我的衣襟，春花、青草的清香偷偷溜入我的衣袖，春雨柔柔地打湿了我的衣衫，踏春归来，襟袖间还飘逸着春的气息。

示例三：踏春归来，襟袖间还飘逸着春的气息，那青草的香味还存留在衣袖间，淡淡地在空气中飘动，那花儿绚烂的色彩还不停地在眼前闪现，那小河奔腾不息的声响还在耳边回荡。

1．扩展以下语句，使语意表达更丰富。(60个字以上)

一首好诗，总是能够最大限度地刺激和调动你的想像。

扩句：________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

[答案]　一首好诗，往往只给你一朵浪花，叫你去想像大海的浩渺；只给你一勾弯月，叫你去想像夜空的宁静；只给你一颗露珠，叫你去想像黎明的清新。它总是能够最大限度地刺激和调动你的想像。

12.已知函数f(x)的定义域为(0，+∞)，且对任意的正实数x，y都有f(xy)＝f(x)+f(y)，且当x＞1时，f(x)＞0，f(4)＝1，

(1)求证：f(1)＝0；

(2)求f()；

(3)解不等式f(x)+f(x－3)≤1.

解：(1)证明：令x＝4，y＝1，则f(4)＝f(4×1)＝f(4)+f(1).∴f(1)＝0.

(2)f(16)＝f(4×4)＝f(4)+f(4)＝2，f(1)＝f(×16)＝f()+f(16)＝0，

故f()＝－2.

(3)设x₁，x₂＞0且x₁＞x₂，于是f()＞0，

∴f(x₁)＝f(×x₂)＝f()+f(x₂)＞f(x₂).

∴f(x)为x∈(0，+∞)上的增函数.

又∵f(x)+f(x－3)＝f[x(x－3)]≤1＝f(4)，

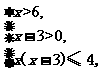∴⇒3＜x≤4.

∴原不等式的解集为{x|3＜x≤4}.

11.已知函数f (x)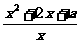＝，x∈[1，+∞).

(1)当a＝4时，求f(x)的最小值；

(2)当a＝时，求f(x)的最小值；

(3)若a为正常数，求f(x)的最小值.

解：(1)当a＝4时，f(x)＝x+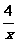+2，易知，f(x)在[1,2]上是减函数，在(2，+∞)上是增函数.

∴f(x)_min＝f(2)＝6.

(2)当a＝时，f(x)＝x+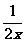+2.

易知，f(x)在[1，+∞)上为增函数.

∴f(x)_min＝f(1)＝.

(3)函数f(x)＝x++2在(0，]上是减函数，在[，+∞)上是增函数.

若>1，即a>1时，f(x)在区间[1，+∞)上先减后增，f(x)_min＝f()＝2+2.

若≤1，即0<a≤1时，

f(x)在区间[1，+∞)上是增函数，

∴f(x)_min＝f(1)＝a+3.

10.已知函数f(x)＝x²－2ax+a，在区间(－∞，1)上有最小值，则函数g(x)＝在区间(1，+∞)上一定　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.有最小值 　　　B.有最大值　　 C.是减函数 　　　　D.是增函数

解析：由题意a<1，又函数g(x)＝x+－2a在[，+∞)上为增函数，故选D.

答案：D

9.设奇函数f(x)在 [－1,1]上是增函数，f(－1)＝－1.若函数f(x)≤t²－2at+1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时，t的取值范围是　　.

解析：若函数f(x)≤t²－2at+1对所有的x∈[－1,1]都成立，由已知易得f(x)的最大值是1，

∴1≤t²－2at+1⇔2at－t²≤0，

设g(a)＝2at－t²(－1≤a≤1)，欲使2at－t²≤0恒成立，

则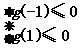⇔t≥2或t＝0或t≤－2.

答案：t≤－2或t＝0或t≥2