
5、一个盒子中有4只白球、2只黑球,从中不放回地每次任取1只,连取2次,求 (1) 第一次取得黑球而第二次取得白球的概率.(2)第一次是白球的情况下,第二次取得白球的概率;
4、 盒子中有25个外形相同的球,其中10个白的,5个黄的,10个黑的,从盒子中任意取出一球,已知它不是黑球,试求他是黄球的概率?
3、一批产品中有4%的次品,而合格品中的一等品占45%,从这批产品中任取一件,求该产品是一等品的概率
1 把一枚硬币任意抛掷两次,事件A=“第一次出现正面”,事件B=“第二次出现正面”,求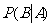 .
.
2、 一个家庭中有两个小孩。假定生男、生女是等可能的,已知这个家庭有一个是女孩,问这时另一个小孩是男孩的概率是多少?
4、 例题分析
类型一:利用概率之比求条件概率
例1 、甲、乙两地都位于长江下游,根据一百多年的气象记录,知道甲、乙两地一年中雨天占的比例分别为20%和18%,两地同时下雨的比例为12%,问:
(1) 乙地为雨天时甲地也为雨天的概率是多少?
(2) 甲地为雨天时乙地也为雨天的概率是多少?
类型二:利用样本点数之比求条件概率
例2、在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2 道题,求:
(l)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第 1 次抽到理科题的条件下,第2次抽到理科题的概率.
例3、。一张储蓄卡的密码共6位数字,每位数字都可从0-9中任选一个.某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过 2 次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率.
类型三:条件概率公式的灵活应用(知二求一)
例4、有外形相同的球分装在三个不同的盒子中,每个盒子10个球,其中第一个盒子中7个球标有字母A,三个球标有字母B;第二个盒子中有红球和白球各5个;第三个盒子中有红球8个,白球2个,试验按如下规则进行:先在第一个盒子中任取一球,若取得标有字母A的球,则在第二个盒子中任取一球;若第一次取得标有字母B的球,则在第三个盒子中任取一球,如果第二次取出的是红球,则试验成功,求试验成功的概率。
3、P(B︱A)的性质:
(1)0  P(B︱A)
P(B︱A) 1
1
(2)若B,C互斥 ,则 P(B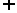 C︱A)= P(B︱A)+ P(C︱A)
C︱A)= P(B︱A)+ P(C︱A)
2、 抛掷一颗质地均匀的骰子所得的样本空间为S={1,2,3,4,5,6},

 令事件B={2,3,5},A={1,2,4,5,6},则 P(A)=
P(B)=
令事件B={2,3,5},A={1,2,4,5,6},则 P(A)=
P(B)=



 P(AB)=
P(B︱A)=
P(B︱A)=
P(AB)=
P(B︱A)=
P(B︱A)=
思考:(1)P(B︱A)与P(AB)的区别和联系
 (2)P(B︱A)+P(B︱A)=1?总成立吗?
(2)P(B︱A)+P(B︱A)=1?总成立吗?
1、由上面抽奖的例子我们可以得到P(B︱A)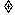 P(B),什么时候可以等?
P(B),什么时候可以等?
2、条件概率定义和公式:
设A和B为两个事件,那么,在“A已发生”的条件下,事件B发生的概率叫做______________________. 用符号___________表示。读作A 发生的条件下 B 发生的概率。
我们把由事件A和B同时发生所构成的事件D,称为事件A与B的___________(或___________),记作___________(或___________)。
一般的,我们有条件概率公式____________________________.
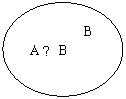
 从集合的角度理解公式:
从集合的角度理解公式:
1、 三张奖券中只有一张能中奖,现分别由三名同学无放回地抽取,问最后一名同学抽到中奖奖券的概率是否比前两名同学小?
解:三张奖券分别用X1,X2,Y,其中Y表示那张中奖奖券,那么三名同学的抽奖结果共有六种可能:__________________________________
最后一名同学抽到中奖奖券的概率为____________
思考:如果已经知道第一名同学没有抽到中奖奖券,那么最后一名同学抽到奖券的概率又是多少?
解:因为已知第一名同学没有抽到中奖奖券,所以可能出现的基本事件只有__________________________________________________
最后一名同学抽到中奖奖券的概率为__________________________
总结:已知第一名同学的抽奖结果为什么会影响最后一名同学抽到中奖奖券的概率呢?
在这个问题中,知道第一名同学没有抽到中奖奖券,等价于知道事件 A 一定会发生,导致可能出现的基本事件必然在事件 A 中,从而影响事件 B 发生的概率。.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com