5、在一密闭容器中有甲、乙、丙、丁四种物质，一定条件下使之反应，一段时间后测得反应前后物质质量如下表所示

则该密闭容器中发生的化学反应类型为

　A、分解反应　　　　　　　　 　　　B、化合反应

C、复分解反应　　　　　　　　　　 D、置换反应

4、下列物质在一定条件下分解，其生成物都是氧化物的是

A、CaCO₃　　　　　　　　　　 B、KMnO₄

C、NH₄HCO₃　　　　　　　　　 D、H₂O

3、推理是化学学习中常用的方法，以下4个推断中正确的是

　 A、氧化物都含有氧元素，所以含有氧元素的化合物一定是氧化物

　 B、酸和碱反应生成盐和水，所以生成盐和水的反应一定是酸与碱的反应

　 C、燃烧一般伴随发热、发光现象，有发热、发光的现象就是燃烧

　 D、化学反应前后各种原子的种类、数目相同，所以反应前后物质的质量总和相同

2、下列物质中，既存在离子又存在分子的是

　 A、金刚石　　　　　　　　 B、氯化钠溶液

　 C、硝酸钾晶体　　　　　　 D、液态氧气

1、下列各组物质中，前者属于单质，后者属于混合物的是

　 A、生铁，稀盐酸　　　　　 B、氢气，碳酸钙

　 C、石墨，空气　　　　　　 D、二氧化碳，蒸馏水

26、(1)抛物线的对称轴为：x=-……………………1分

∵抛物线经过点C(0,-)

∴C＝-……………………………………………………………2分

(2)由题意得：X₁，X₂是方程ax²+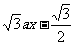=0的两根……………1分

∴X₁+X₂=-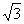,X₁·X₂=-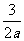

又∵AB=x₁-x₂=2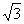

∴(X₂-X₁)²＝12

(X₁+X₂)²-4X₁X₂=12

∴3+4×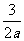=12

∴a=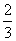………………………………………………………………5分

∴抛物线的解析式为y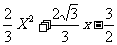＝………………………6分

(3)在y=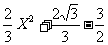中，令y＝0，得

4x²+4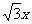-9＝0

解得：X₁=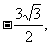X₂＝

∴A(-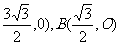………………………………………7分

过D作DE⊥y轴于E

∵∠OPB＝∠EPD，∠POB＝∠PED，PB=PD

∴△BOP≌△DEP(SAS)

∴DE=OB

∴D点的横坐标为-

∴D点在抛物线的对称轴X=上…………………………8分

设⊙P的半径为R，则有：(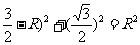

∴R=1　　　　 ∴OP＝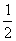

∴PE＝OP＝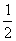

∴D(-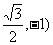……………………………………………………10分

设过D点⊙P的切线交y轴于F

∵DF为⊙P切线

∴∠PDF＝90°

又∵DE⊥y轴

∴△PDE∽△DEF

DE²＝PE·EF

∴EF=

∴F(0,-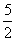)……………………………………………………12分

设直线DF的解析式为y=kx+b

∴

∴

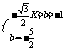
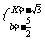
∴直线DF的解析式为：y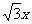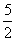＝--…………………………13分

本资料由《七彩教育网》 提供！

25、解：(1)S₁=S₂+S₃………………………………………………………2分

(2)S₁、S₂、S₃之间的关系为：S₁=S₂+S₃…………………………3分

证明：∵S₁＝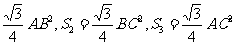

∴S₂+S₃=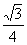(AC²+AB²)

又：AC²+BC²=AB²

∴S₂+S₃=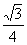AB²＝S₁…………………………………………6分

(3)所作的三角形应满足：是以AB、BC、AC为对应边的三个相似三角形……7分

证明：∵=(＝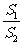

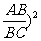∴S₂=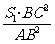

同理：S₃=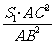

∴S₂+S₃=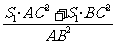=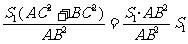…………10分

(4)向形外以AB、BC、AC为对应边作三个相似的图形

则有S₁=S₂+S₃…………………………………………………………12分

说明：(3)中只要学生说到相似三角形即可。

(4)中同样说明相似图形即可(对应边不一定指出)。

解：(1)∵方程有两根

∴△＝(2m-1)²-4m²

＝4m²-4m+1-4m²

＝-4m+1≥0

∴m≤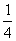…………………………………………………………3分

(2)∵x₁²-x₂²=0

∴(x₁+x₂)(x₁-x₂)=0

∴x₁+x₂＝0或x₁＝x₂……………………………………………4分

当X₁+X₂＝0时，

有-(2m-1)＝0

∴m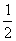＝(不合题意)…………………………………………6分

当X₁=X₂时

有-4m+1＝0

∴m＝………………………………………………………… 9分

所以，m的值为。……………………………………………10分

24、解：(1)证明：∵AB=AC

∴∠ABC=∠C

又∵∠ADB=∠C

∴∠ADB=∠ABC

又∵BC∥ED

∴∠ABC=∠E

∴∠ADB=∠E………………………………………………3分

(2)当D点是劣弧BC弧的中点时，DE是⊙O的切线………………4分

理由：当D点是弧BC的中点时，则有AD⊥BC，且AD过圆心O……5分

又∵DE∥BC

∴AD⊥DE

∴DE是⊙O的切线………………………………………6分

(3)如图，连结OA、OB，延长AO交BC于F.

∴AF⊥BC，BF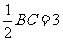＝…………………………………7分

又∵AB=5

∴AF＝4………………………………………………… 8分

设⊙O半径为r

OF＝4-r,OB＝r，BF＝3

∴r²=3²+(4-r)²……………………………………………10分

解得：r=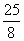

⊙O的半径为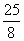…………………………………………10分

22、解：(1)在Rt△ABC中　

∵AB=BC·tan∠ACB

∴AB＝60×tan30°

＝60×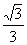

＝20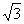(米)…………………………………………………4分

　　　　　 (2)在Rt△BDC中

∵BC=DC·tan∠BDC

＝a×tan60°

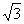＝a(米)…………………………………………………7分

　　　　　　 又在Rt△ABC中

　AB＝BC·tan∠ACB

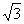　 ＝a·tan30°

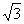　 ＝a·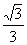

　 ＝a(米)………………………………………………………10分

说明：计算过程中不带单位适当扣分；其中(2)问可利用全等解决。

21、解：(1)解析式为：y=2x+2………………………………………………2分

在y=2x+2中，令x＞0，得y＝2

∴B(0，2) ……………………………………………………3分

(2)∵∠ABP＝90°，∠AOB＝90°

∴易得△AOB∽△BOP

∴OB²＝OA·OP

∴OP＝4

∴P(0，4)……………………………………………………6分

(3)∵MN∥BP

∴△OMN∽△OBP ………………………………………………8分

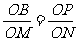∴……………………………………………………9分

∴

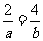
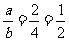∴……………………………………………………10分