
6、诱导公式:奇变偶不变,符号看象限。如:
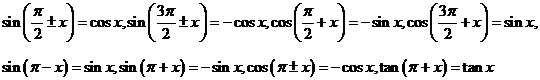
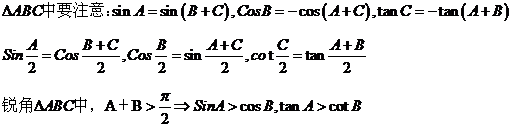
熟记关系式:sin(kπ+α)=(-1)ksinα;cos(kπ+α)=(-1)kcosα(k∈Z).
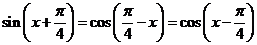 ;
;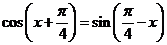
5、象限角的三角函数符号:一全正,二正弦,三两切,四余弦。
根据三角函数线分析各象限的区间内各三角函数的单调性:正弦一,四增,二、三减。余弦三、四增,一、二减。正切只有增区间,余切只有减区间。强调象限的区间内。
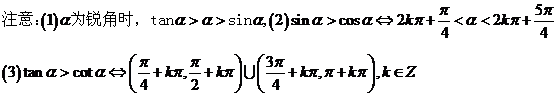
4、任意角的三角函数的定义:设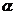 是任意一个角,
是任意一个角,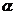 的终边上任意一点P的坐标是(x,y),它与原点的距离是
的终边上任意一点P的坐标是(x,y),它与原点的距离是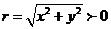 ,那么
,那么
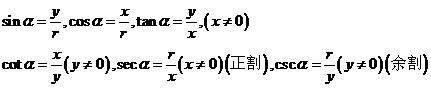
3、角度制与弧度制的换算: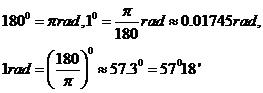
弧度制下的弧长与扇形面积计算公式: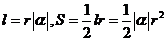
注:在同一个代数式中弧度制与角度制不能同时出现。如: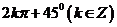 是错误的。
是错误的。
2、终边相同的角的表示:
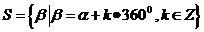 ,即任一与角
,即任一与角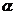 终边相同的角,都可以表成角
终边相同的角,都可以表成角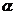 与整数个周角的和。任意两个终边相同的角之差必是360°的整数倍。相等的角的终边一定相同,终边相同的角不一定相等。
与整数个周角的和。任意两个终边相同的角之差必是360°的整数倍。相等的角的终边一定相同,终边相同的角不一定相等。
已知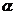 是第几象限的角,如何确定
是第几象限的角,如何确定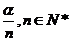 所在象限的角的常用方法有二:(1)分类讨论法,先根据
所在象限的角的常用方法有二:(1)分类讨论法,先根据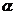 的范围用整数k把
的范围用整数k把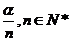 的范围表示出来,再对k分n种情况讨论。(2)几何法:把各象限均先n等分,再从x轴的正方向的上方起,依次将各区域标上①、②、③、④,则
的范围表示出来,再对k分n种情况讨论。(2)几何法:把各象限均先n等分,再从x轴的正方向的上方起,依次将各区域标上①、②、③、④,则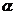 原来是第几象限对应的标号即为
原来是第几象限对应的标号即为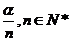 的终边所在的区域。
的终边所在的区域。
1、象限角与轴线角:角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限,称为轴线角。第一、二、三、四象限角分别可表示为:
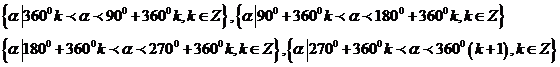
角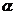 终边在x轴的非负半轴上时可表示为:
终边在x轴的非负半轴上时可表示为: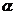 =360°k,k∈Z, 角
=360°k,k∈Z, 角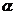 终边在y轴的非负半轴上时可表示为:
终边在y轴的非负半轴上时可表示为: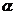 =360°k+90°,k∈Z,在x轴的非正方向上,在y轴的非正方向上可类似表示。
=360°k+90°,k∈Z,在x轴的非正方向上,在y轴的非正方向上可类似表示。
6、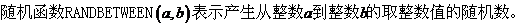

用随机模拟计算阴影面积的方法与步骤:

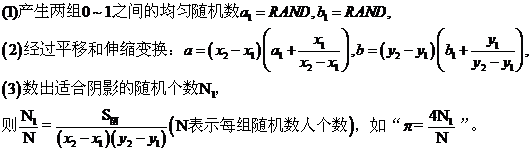
第十四讲三角函数的概念、诱导公式与二倍解公式
5、 几何概型:如果每个事件发生的概率只有与构成该事件区域的长度(面积或体积)成比例,称这样的概率模型为几何概型。计算公式是:
4、 关于古典概型:基本事件的特点是:任何两个基本事件是互斥的,任何事件(不可能事件除外)都可以表示为基本事件的和。若试验中可能出现的基本事件只有有限种,且每个基本事件出现的可能性相同,具有这两个特征的概率模型称为古典概型。对于古典概型:
3、 概率的几个性质:
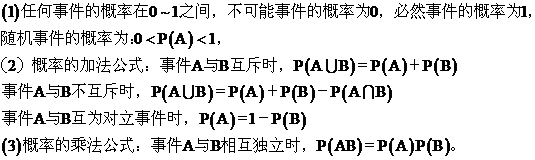
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com