
1 已知tan(α+β)=
已知tan(α+β)=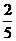 ,tan(β-
,tan(β-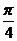 )=
)=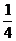 ,那么tan(α+
,那么tan(α+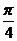 )等于
)等于

2 在△ABC中,已知tanA,tanB是方程3x2+8x-1=0的两个根,则tanC等于( )
在△ABC中,已知tanA,tanB是方程3x2+8x-1=0的两个根,则tanC等于( )
A 2
B
2
B -2
C
-2
C 4
D
4
D -4
-4
3 在△ABC中,若0<tanA·tanB<1则△ABC一定是( )
在△ABC中,若0<tanA·tanB<1则△ABC一定是( )
A 等边三角形 B
等边三角形 B 直角三角形
C
直角三角形
C 锐角三角形 D
锐角三角形 D 钝角三角形
钝角三角形
4
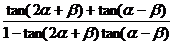 =
=

5 (1+tan10°)·(1+tan35°)=
(1+tan10°)·(1+tan35°)=

6 在△ABC中,tanA=
在△ABC中,tanA=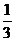 ,tanB=-2,则C=
,tanB=-2,则C=

7 已知tanα、tanβ是方程x2-5x+6=0的两个实根,求2sin2(α+β)-3sin(α+β)cos(α+β)+cos2(α+β)
已知tanα、tanβ是方程x2-5x+6=0的两个实根,求2sin2(α+β)-3sin(α+β)cos(α+β)+cos2(α+β)
1 设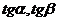 是一元二次方程
是一元二次方程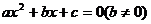 的两个根,求
的两个根,求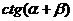 的值.
的值.
分析:易知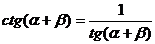 ,联想公式(
,联想公式(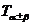 )与韦达定理求解
归纳:如果已知
)与韦达定理求解
归纳:如果已知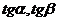 是一元二次方程
是一元二次方程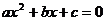 的两个根,那么联想公式
的两个根,那么联想公式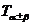 与韦达定理便于探求结论.
与韦达定理便于探求结论.
2 已知
已知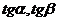 是一元二次方程
是一元二次方程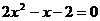 的两个根,求
的两个根,求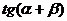 的值.
的值.
1 已知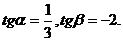
(1)求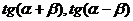 ;
;
(2)求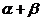 的值(其中
的值(其中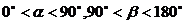 ).
).
分析:
(1)观察(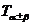 )的结构,直接代入公式;若改求
)的结构,直接代入公式;若改求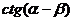 呢?
呢?
(2)由(1)直接运用公式(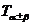 )容易求出
)容易求出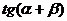 的值.但由已知的三角函数值求角时,所得的解不唯一的.因此,必须根据已知条件进行分析,这就要确定
的值.但由已知的三角函数值求角时,所得的解不唯一的.因此,必须根据已知条件进行分析,这就要确定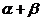 的范围.
的范围.
2 计算下列各式的值
(1)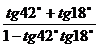 (2)
(2)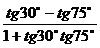
分析:观察探求的结构,可以逆用公式(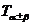 )求解.
)求解.
3 计算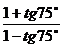 的值.
的值.
分析:因为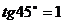 ,所以原式可以看成是
,所以原式可以看成是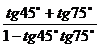
例1求tan15°,tan75°及cot15°的值:
解:1° tan15°=
tan(45°-30°)= 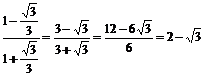
2° tan75°= tan(45°+30°)= 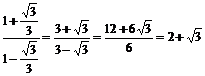
3° cot15°= cot(45°-30°)= 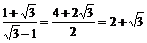
例2 已知tana=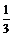 ,tanb=-2 求cot(a-b),并求a+b的值,其中0°<a<90°, 90°<b<180°
,tanb=-2 求cot(a-b),并求a+b的值,其中0°<a<90°, 90°<b<180° 
解:cot(a-b)=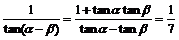
∵ tan(a+b)=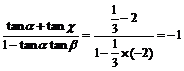
且∵0°<a<90°, 90°<b<180° ∴90°<a+b<270° ∴a+b=135°
例3 求下列各式的值:
1° 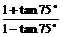 2°tan17°+tan28°+tan17°tan28°
2°tan17°+tan28°+tan17°tan28°
解:1°原式=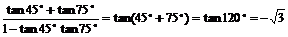
2° ∵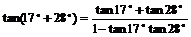
∴tan17°+tan28°=tan(17°+28°)(1-tan17°tan28°)=1- tan17°tan28°
∴原式=1- tan17°tan28°+ tan17°tan28°=1
3.引导学生自行推导出cot(a±b)的公式-用cota,cotb表示
cot(a+b)=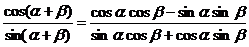
当sinasinb¹0时,cot(a+b)=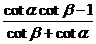
同理,得:cot(a-b)=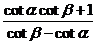
两角和与差的正切公式 Ta+b ,Ta-b
1 tan(a+b)公式的推导
tan(a+b)公式的推导
∵cos (a+b)¹0
tan(a+b)=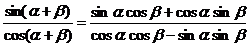
当cosacosb¹0时, 分子分母同时除以cosacosb得:
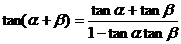
以-b代b得: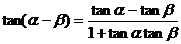
其中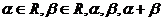 都不等于
都不等于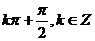
2.注意:1°必须在定义域范围内使用上述公式
即:tana,tanb,tan(a±b)只要有一个不存在就不能使用这个公式,只能(也只需)用诱导公式来解
2°注意公式的结构,尤其是符号
2.已知sina+sinb=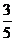 ① , cosa+cosb=
① , cosa+cosb=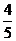 ② ,求cos(a-b)
② ,求cos(a-b)
解: ①2: sin2a+2sinasinb+sin2b=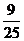 ③
③
②2: cos2a+2cosacosb+cos2b=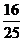 ④
④
③+④: 2+2(cosacosb+sinasinb)=1
即:cos(a-b)=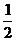
2.求证:cosx+sinx=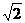 cos(x
cos(x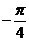 )
)
证:左边= 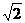 (
(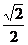 cosx+
cosx+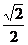 sinx)=
sinx)=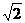 ( cosxcos
( cosxcos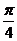 +sinxsin
+sinxsin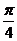 )
)
=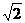 cos(x
cos(x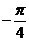 )=右边
)=右边
又证:右边=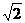 ( cosxcos
( cosxcos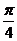 +sinxsin
+sinxsin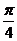 )=
)=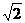 (
(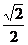 cosx+
cosx+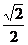 sinx)
sinx)
= cosx+sinx=左边
1.两角和与差的正、余弦公式
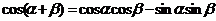
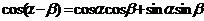
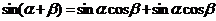
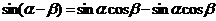
20. [解]:(1)当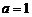 时,
时,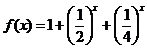
因为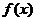 在
在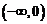 上递减,所以
上递减,所以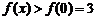 ,即
,即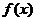 在
在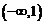 的值域为
的值域为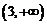
故不存在常数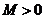 ,使
,使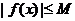 成立
成立
所以函数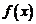 在
在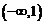 上不是有界函数。 ……………4分(没有判断过程,扣2分)
上不是有界函数。 ……………4分(没有判断过程,扣2分)
(2)由题意知,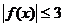 在
在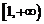 上恒成立。………5分
上恒成立。………5分
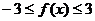 ,
, 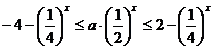
∴ 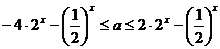 在
在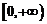 上恒成立………6分
上恒成立………6分
∴
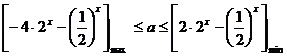 ………7分
………7分
设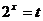 ,
,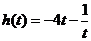 ,
,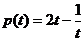 ,由
,由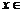
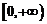 得 t≥1,
得 t≥1,
设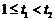 ,
,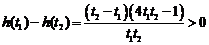
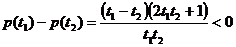
所以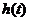 在
在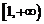 上递减,
上递减,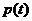 在
在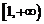 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
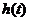 在
在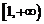 上的最大值为
上的最大值为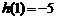 ,
, 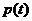 在
在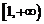 上的最小值为
上的最小值为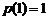
所以实数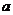 的取值范围为
的取值范围为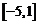 。…………………………………10分
。…………………………………10分
(3)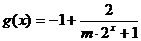 ,
,
∵ m>0 ,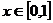 ∴
∴ 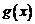 在
在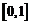 上递减,
上递减,
∴ 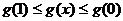 即
即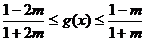 ………12分
………12分
①当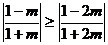 ,即
,即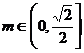 时,
时,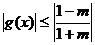 ,
,
此时 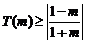 ,………14分
,………14分
②当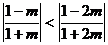 ,即
,即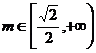 时,
时,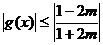 ,
,
此时 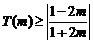 ,
,
综上所述,当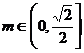 时,
时,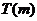 的取值范围是
的取值范围是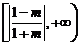 ;
;
当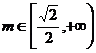 时,
时,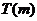 的取值范围是
的取值范围是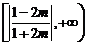 ………16
………16
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com