
9、(2009广州)已知:A、B、C是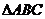 的内角,
的内角,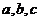 分别是其对边长,向量
分别是其对边长,向量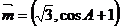 ,
,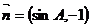 ,
,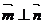 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若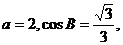 求
求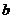 的长.
的长.
解:(Ⅰ)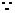
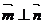
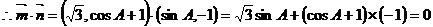
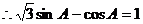 ……4分
……4分
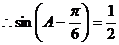 ……6分
……6分
∵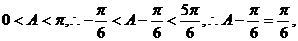 ……7分
……7分
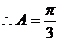 .……8分
.……8分
(Ⅱ)在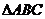 中,
中,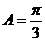 ,
,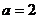 ,
,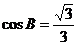
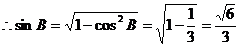 ……9分
……9分
由正弦定理知: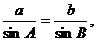 ……10分
……10分

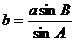 =
=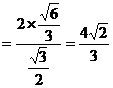 .
.
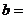
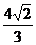 ……12分
……12分
8、(2009广东六校)设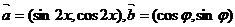
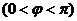 ,函数
,函数 且
且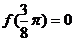 .
.
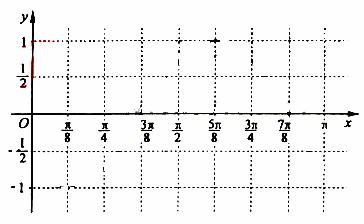
(Ⅰ)求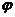 ;(Ⅱ)在给出的直角坐标系中画出函数
;(Ⅱ)在给出的直角坐标系中画出函数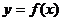 在区间
在区间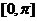 上的图像;
上的图像;
(Ⅲ)根据画出的图象写出函数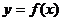 在
在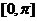 上的单调区间和最值.
上的单调区间和最值.
解:  =
=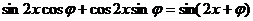 2分
2分
由题可知: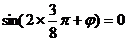 ,
3分
,
3分
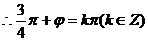 ,
4分
,
4分
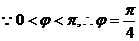 5分
5分
(2)
9分
(3)单调增区间: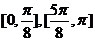 10分
10分
单调减区间: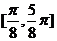 11分
11分
函数的最大值是:1
函数的最小值是: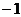 12分
12分
7、(2009饶平)已知向量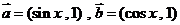 。
。
(1) 当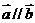 时,求
时,求 的值;
的值;
(2) 求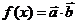 的最小正周期。
的最小正周期。
解:(1)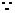
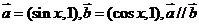 ,∴
,∴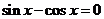 …..3分
…..3分
 。…………………6分
。…………………6分
(2)由已知可得: ………..11分
………..11分
∴ f(x)的最小正周期为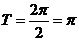 …………12分
…………12分
6、(2009中山)已知向量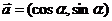 ,
, 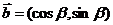 ,
,  .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
, 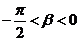 , 且
, 且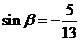 , 求
, 求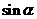 .
.
解:(Ⅰ)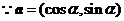 ,
, 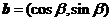 ,
,
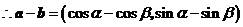 . ……………2分
. ……………2分
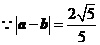 ,
, 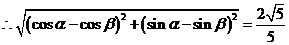 , ………3分
, ………3分
即 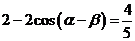 , ………5分
, ………5分 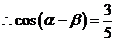 . ……………6分
. ……………6分
(Ⅱ)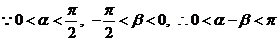 , ……………7分
, ……………7分
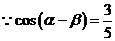 ,
, 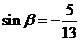
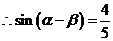 ,
, 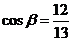 ……………9分
……………9分 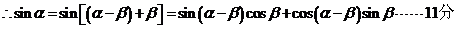
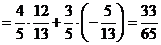 . ……………12分
. ……………12分
5、(2009潮州)函数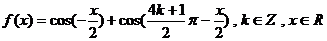 。
。
(1)求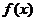 的周期;(2)解析式及
的周期;(2)解析式及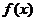 在
在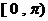 上的减区间;
上的减区间;
(3)若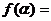
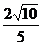 ,
,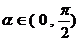 ,求
,求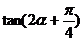 的值。
的值。
解:(1)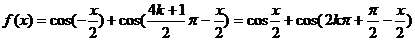
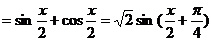 ,(
,(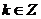 )
)
所以,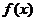 的周期
的周期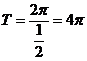 。 …… 4分
。 …… 4分
(2)由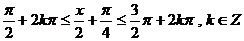 ,得
,得 。
。
又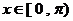 ,
,
令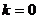 ,得
,得
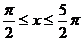 ;令
;令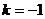 ,得
,得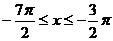 (舍去)
(舍去)
∴
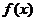 在
在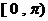 上的减区间是
上的减区间是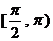 。 …… 8分
。 …… 8分
(3)由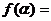
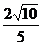 ,得
,得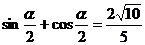 ,
,
∴ 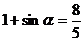 , ∴
, ∴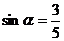
又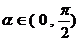 ,∴
,∴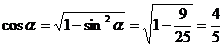
∴ 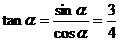 ,∴
,∴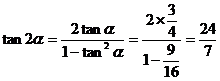
∴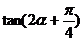
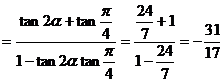 。
……12分
。
……12分
4、(2009珠海)已知函数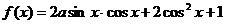 ,
,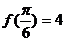 ,
,
(1)求实数a的值;
(2)求函数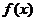 在
在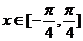 的值域。
的值域。
解: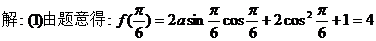 ,
,
即: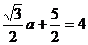 ,………………………..2分
,………………………..2分
解得: ;
;
 。……………………………..3分
。……………………………..3分
(2)由(1)得: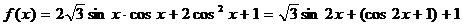
……………….…..5分
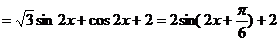 ………….…………7分
………….…………7分
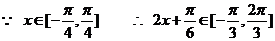 ,…………………………………………..8分
,…………………………………………..8分
令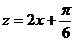 ,则
,则 ,…10分
,…10分
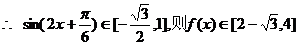 ,
,
即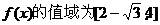 …………………………….12分
…………………………….12分
3、(2009广东四校)已知函数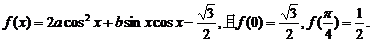
(1)求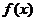 的最小正周期;
的最小正周期;
(2)求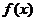 的单调递增区间.
的单调递增区间.
解:(1) 由 f (0) = 得a= ,
由 f ( ) = 得b=1
∴ f (x) =cos2x+sin x cos x-
= cos 2x + sin 2x = sin(2x+ )
故最小正周期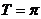 6分
6分
(2) 由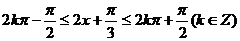
得 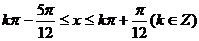
故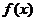 的单调递增区间为
的单调递增区间为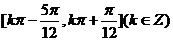 12分
12分
2、(2009揭阳)在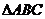 中,
中,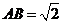 ,
, ,
,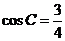 .
.
(Ⅰ)求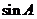 的值;
的值;
(Ⅱ)求 的值.
的值.
解:(1)在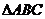 中,由
中,由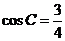 ,得
,得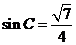 …………………………2分
…………………………2分
又由正弦定理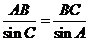 ………………………………………3分
………………………………………3分
得: …………………………………………………………………………………4分
…………………………………………………………………………………4分
(2)由余弦定理: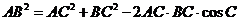 得:
得: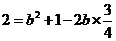 ……6分
……6分
即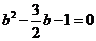 ,解得
,解得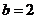 或
或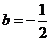 (舍去),所以
(舍去),所以 ………………8分
………………8分
所以,
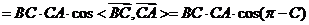 ……………10分
……………10分
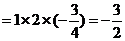 ,即
,即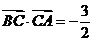 ……………… ……12分
……………… ……12分
1、(2009揭阳)已知:函数 .
.
(1)求函数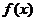 的最小正周期和值域;
的最小正周期和值域;
(2)若函数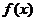 的图象过点
的图象过点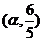 ,
, .求
.求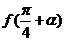 的值.
的值.
解:(1)
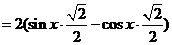
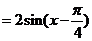 ---3分
---3分
∴函数的最小正周期为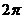 ,值域为
,值域为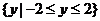 。--------------------------------------5分
。--------------------------------------5分
(2)解:依题意得: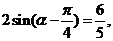
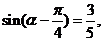 ---------------------------6分
---------------------------6分
∵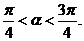 ∴
∴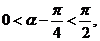
∴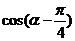 =
=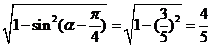 -----------------------------------------8分
-----------------------------------------8分
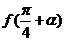 =
=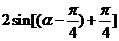
∵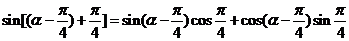 =
=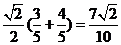
∴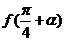 =
=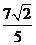 ------------------------------------------------------------------------------12分
------------------------------------------------------------------------------12分
9、(2009韶关田家炳)已知平面向量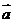 =
=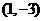 ,
,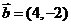 ,若
,若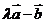 与
与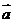 垂直,则
垂直,则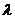 =( )B
=( )B
A.-1 B.1 C.-2 D.2
10、(2009汕头潮南)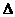 ABC的三边分别为a,b,c且满足
ABC的三边分别为a,b,c且满足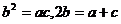 ,则此三角形是( )D
,则此三角形是( )D
(A)等腰三角形 (B)直角三角形 (C)等腰直角三角形 (D)等边三角形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com