
10. 定义在R上的函数f(x)满足f(x)= 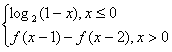 ,则f(2009)的值为( )
,则f(2009)的值为( )
A.-1 B. 0 C.1 D. 2
[解析]:由已知得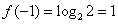 ,
,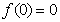 ,
,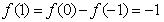 ,
,
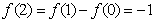 ,
,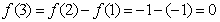 ,
,
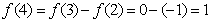 ,
,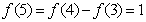 ,
,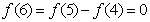 ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
答案:C.
[命题立意]:本题考查归纳推理以及函数的周期性和对数的运算.
9. 设双曲线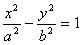 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x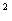 +1 只有一个公共点,则双曲线的离心率为( ).
+1 只有一个公共点,则双曲线的离心率为( ).
A. 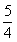 B.
5 C.
B.
5 C.
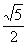 D.
D.
[解析]:双曲线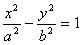 的一条渐近线为
的一条渐近线为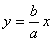 ,由方程组
,由方程组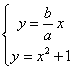 ,消去y,得
,消去y,得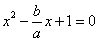 有唯一解,所以△=
有唯一解,所以△=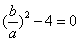 ,
,
所以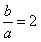 ,
,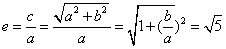 ,故选D.
,故选D.
答案:D.
[命题立意]:本题考查了双曲线的渐近线的方程和离心率的概念,以及直线与抛物线的位置关系,只有一个公共点,则解方程组有唯一解.本题较好地考查了基本概念基本方法和基本技能.
8.某工厂对一批产品进行了抽样检测.有图是根据抽样检测后的
产品净重(单位:克)数据绘制的频率分布直方图,其中产品
净重的范围是[96,106],样本数据分组为[96,98),[98,100),
[100,102),[102,104),[104,106],已知样本中产品净重小于
100克的个数是36,则样本中净重大于或等于98克并且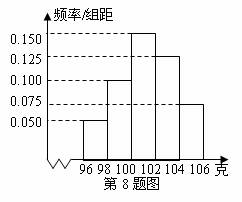
小于104克的产品的个数是( ).
A.90 B.75 C. 60 D.45
[解析]:产品净重小于100克的概率为(0.050+0.100)×2=0.300,
已知样本中产品净重小于100克的个数是36,设样本容量为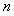 ,
,
则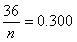 ,所以
,所以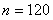 ,净重大于或等于98克并且小于
,净重大于或等于98克并且小于
104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本
中净重大于或等于98克并且小于104克的产品的个数是
120×0.75=90.故选A.
答案:A
[命题立意]:本题考查了统计与概率的知识,读懂频率分布直方图,会计算概率以及样本中有关的数据.
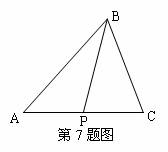
7.设P是△ABC所在平面内的一点,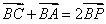 ,则( )
,则( )
A.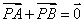 B.
B.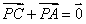 C.
C.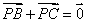 D.
D.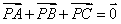
[解析]:因为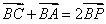 ,所以点P为线段AC的中点,所以应该选C。
,所以点P为线段AC的中点,所以应该选C。
答案:C。
[命题立意]:本题考查了向量的加法运算和平行四边形法则,
可以借助图形解答。
5. 已知α,β表示两个不同的平面,m为平面α内的
一条直线,则“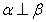 ”是“
”是“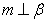 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
[解析]:由平面与平面垂直的判定定理知如果m为平面α内的
一条直线,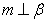 ,则
,则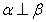 ,反过来则不一定.所以“
,反过来则不一定.所以“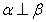 ”是“
”是“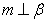 ”的必要不充分条件.
”的必要不充分条件.
答案:B.
[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
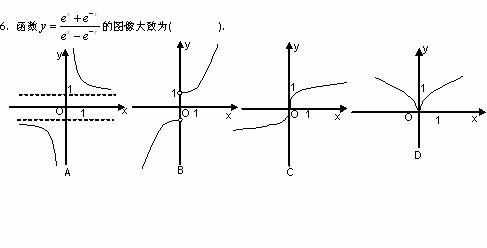
[解析]:函数有意义,需使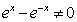 ,其定义域为
,其定义域为 ,排除C,D,又因为
,排除C,D,又因为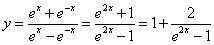 ,所以当
,所以当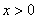 时函数为减函数,故选A.
时函数为减函数,故选A.
答案:A.
[命题立意]:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
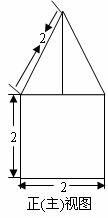
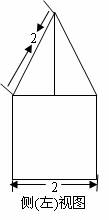
4. 一空间几何体的三视图如图所示,则该几何体的体积为( ).
A.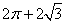 B.
B. 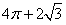 C.
C.
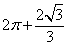 D.
D.
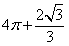
[解析]:该空间几何体为一圆柱和一四棱锥组成的,
圆柱的底面半径为1,高为2,体积为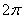 ,四棱锥的底面
,四棱锥的底面
边长为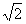 ,高为
,高为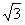 ,所以体积为
,所以体积为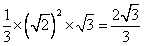
所以该几何体的体积为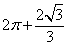 .
.
答案:C
[命题立意]:本题考查了立体几何中的空间想象能力,
 由三视图能够想象得到空间的立体图,并能准确地
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
3. [解析]:将函数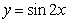 的图象向左平移
的图象向左平移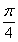 个单位,得到函数
个单位,得到函数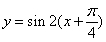 即
即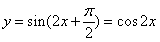 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为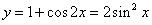 ,故选D.
,故选D.
答案:D
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
3.将函数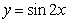 的图象向左平移
的图象向左平移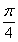 个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
个单位, 再向上平移1个单位,所得图象的函数解析式是(
).
A.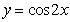 B.
B.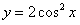 C.
C.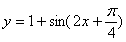 D.
D.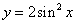
2. [解析]:
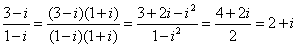 ,故选C.
,故选C.
答案:C
[命题立意]:本题考查复数的除法运算,分子、分母需要同乘以分母的共轭复数,把分母变为实数,将除法转变为乘法进行运算.
2.复数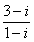 等于( ).
等于( ).
A.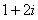 B.
B.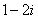 C.
C.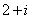 D.
D.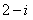
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com