20.(本题满分16分)

已知等差数列的公差是，是该数列的前项和.

(1)试用表示，其中均为正整数；

(2)利用(1)的结论求解：“已知，求”；

(3)若各项均为正数的等比数列的公比为，前项和为，试类比问题(1)的结论，写出一个相应的结论且给出证明，并利用此结论求解问题：“已知各项均为正数的等比数列，其中，求数列的前50项和.”

2011届高三暑假自主学习调查

数　 学　　　　 　2010.9

附加题

19.(本题满分16分)

已知函数，.

(1)若函数存在单调递减区间，求的取值范围；

(2)令，是否存在实数，当时，函数的最小值是3，若存在，求出的值；若不存在，请说明理由.

18.(本小题满分15分)

某企业有两个生产车间分别在A，B两个位置，A车间有100名员工，B车间有400名员工，现要在公路AC上找一点D，修一条公路BD，并在D处建一个食堂，使得所有员工均在此食堂用餐，已知A，B，C中任意两点间的距离均有1km，设∠BDC＝α，所有员工从车间到食堂步行的总路程为S．

(1)写出S关于α的函数表达式，并指出α的取值范围；

(2)问食堂D建在距离A多远时，可使总路程S最少？

17.(本题满分15分)

已知椭圆的离心率为，一条准线为，若椭圆与轴交于两点，是椭圆上异于的任意一点，直线交直线于点，直线交直线于点，记直线的斜率分别为.

　 (1)求椭圆的方程；

(2)求的值；

(3)求证：以为直径的圆过轴上的定点，并求出定点的坐标.

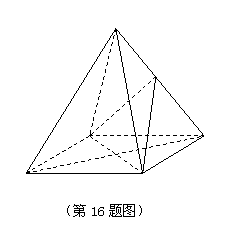
16.(本题满分14分)

在四棱锥中，底面是菱形，为正三角形，为侧棱上一点.

(1)当为侧棱的中点时，求证：平面；

(2)求证：平面平面.

15.(本题满分14分)

已知向量，向量，且，与的夹角为.

(1)求；

(2)若向量，且，求实数的值.

14.设函数的定义域为，若存在非零实数，使得对于任意，有，且，则称为上的高调函数，如果定义域是的函数为上的高调函数，那么实数的取值范围是　 ▲　 ．

13.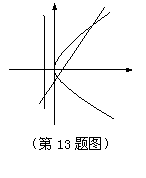如图，过抛物线的焦点F的直线交抛物线于点，交其准线于点，若，且，则此抛物线的方程为　 ▲　 ．

12.在数列中，，则　 ▲　 ．

11.函数在定义域内可导，若，且当时，则，，的大小关系是(要求用“”连结)　 ▲　 ．