
2.探索新知
一般地,我们把函数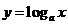 (
( >0且
>0且 ≠1)叫做对数函数,其中
≠1)叫做对数函数,其中 是自变量,函数的定义域是(0,+∞).
是自变量,函数的定义域是(0,+∞).
提问:(1).在函数的定义中,为什么要限定 >0且
>0且 ≠1.
≠1.
(2).为什么对数函数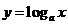 (
( >0且
>0且 ≠1)的定义域是(0,+∞).组织学生充分讨论、交流,使学生更加理解对数函数的含义,从而加深对对数函数的理解.
≠1)的定义域是(0,+∞).组织学生充分讨论、交流,使学生更加理解对数函数的含义,从而加深对对数函数的理解.
答:①根据对数与指数式的关系,知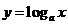 可化为
可化为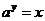 ,由指数的概念,要使
,由指数的概念,要使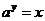 有意义,必须规定
有意义,必须规定 >0且
>0且 ≠1.
≠1.
②因为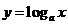 可化为
可化为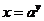 ,不管
,不管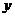 取什么值,由指数函数的性质,
取什么值,由指数函数的性质,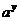 >0,所以
>0,所以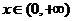 .
.
例题1:求下列函数的定义域
(1)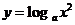 (2)
(2)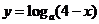 (
( >0且
>0且 ≠1)
≠1)
分析:由对数函数的定义知: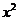 >0;
>0; >0,解出不等式就可求出定义域.
>0,解出不等式就可求出定义域.
解:(1)因为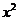 >0,即
>0,即 ≠0,所以函数
≠0,所以函数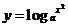 的定义域为
的定义域为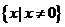 .
.
(2)因为 >0,即
>0,即 <4,所以函数
<4,所以函数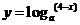 的定义域为
的定义域为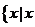 <
<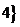 .
.
下面我们来研究函数的图象,并通过图象来研究函数的性质:
先完成P81表2-3,并根据此表用描点法或用电脑画出函数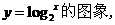 再利用电脑软件画出
再利用电脑软件画出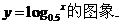
 |
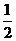 |
1 |
2 |
4 |
6 |
8 |
12 |
16 |
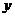 |
-1 |
0 |
1 |
2 |
2.58 |
3 |
3.58 |
4 |
 y
y
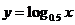
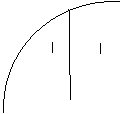

0 x
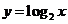
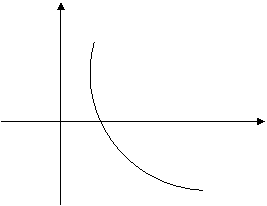
注意到: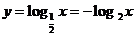 ,若点
,若点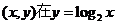 的图象上,则点
的图象上,则点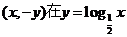 的图象上. 由于(
的图象上. 由于(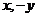 )与(
)与(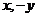 )关于
)关于 轴对称,因此,
轴对称,因此,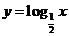 的图象与
的图象与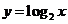 的图象关于
的图象关于 轴对称 . 所以,由此我们可以画出
轴对称 . 所以,由此我们可以画出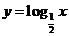 的图象 .
的图象 .
先由学生自己画出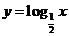 的图象,再由电脑软件画出
的图象,再由电脑软件画出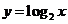 与
与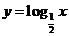 的图象.
的图象.
探究:选取底数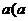 >0,且
>0,且 ≠1)的若干不同的值,在同一平面直角坐标系内作出相应的对数函数的图象.观察图象,你能发现它们有哪些特征吗?
≠1)的若干不同的值,在同一平面直角坐标系内作出相应的对数函数的图象.观察图象,你能发现它们有哪些特征吗?
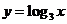 .作法:用多媒体再画出
.作法:用多媒体再画出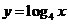 ,
,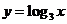 ,
,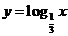 和
和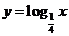
|
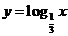
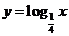

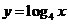
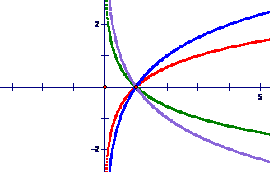
提问:通过函数的图象,你能说出底数与函数图象的关系吗?函数的图象有何特征,性质又如何?
先由学生讨论、交流,教师引导总结出函数的性质. (投影)
|
图象的特征 |
函数的性质 |
(1)图象都在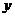 轴的右边 轴的右边 |
(1)定义域是(0,+∞) |
|
(2)函数图象都经过(1,0)点 |
(2)1的对数是0 |
(3)从左往右看,当 >1时,图象逐渐上升,当0< >1时,图象逐渐上升,当0< <1时,图象逐渐下降 . <1时,图象逐渐下降 . |
(3)当 >1时, >1时,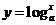 是增函数,当 是增函数,当0<  <1时, <1时,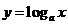 是减函数. 是减函数. |
(4)当 >1时,函数图象在(1,0)点右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0.
当0< >1时,函数图象在(1,0)点右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0.
当0< <1时,图象正好相反,在(1,0)点右边的纵坐标都小于0,在(1,0)点左边的纵坐标都大于0 . <1时,图象正好相反,在(1,0)点右边的纵坐标都小于0,在(1,0)点左边的纵坐标都大于0 . |
(4)当 >1时 >1时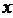 >1,则 >1,则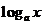 >0 >00< 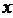 <1, <1,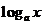 <0 <0当0<  <1时 <1时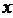 >1,则 >1,则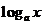 <0 <00< 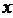 <1, <1,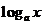 <0 <0 |
由上述表格可知,对数函数的性质如下(先由学生仿造指数函数性质完成,教师适当启发、引导):
|
|
 >1 >1 |
0< <1 <1 |
|
图 象 |
|
|
|
性 质 |
(1)定义域(0,+∞); (2)值域R; (3)过点(1,0),即当  =1, =1,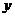 =0; =0; |
|
|
(4)在(0,+∞)上是增函数 |
在(0,+∞)是上减函数 |
例题训练:
1.设置情境
在2.2.1的例6中,考古学家利用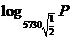 估算出土文物或古遗址的年代,对于每一个C14含量P,通过关系式,都有唯一确定的年代
估算出土文物或古遗址的年代,对于每一个C14含量P,通过关系式,都有唯一确定的年代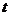 与之对应.同理,对于每一个对数式
与之对应.同理,对于每一个对数式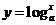 中的
中的 ,任取一个正的实数值,
,任取一个正的实数值,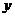 均有唯一的值与之对应,所以
均有唯一的值与之对应,所以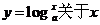 的函数.
的函数.
2、难点:底数a对图象的影响及对数函数性质的作用.
1、重点:理解对数函数的定义,掌握对数函数的图象和性质.
2.教学手段:多媒体计算机辅助教学.
1.学法:通过让学生观察、思考、交流、讨论、发现函数的性质;
3.情感、态度与价值观
①培养学生数形结合的思想以及分析推理的能力;
②培养学生严谨的科学态度.
2.过程与方法
让学生通过观察对数函数的图象,发现并归纳对数函数的性质.
1.知识技能
①对数函数的概念,熟悉对数函数的图象与性质规律.
②掌握对数函数的性质,能初步运用性质解决问题.
2、思考:(1)证明和应用对数运算性质时,应注意哪些问题?
(2)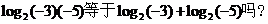
§2.2.2对数函数及其性质(第一、二课时)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com