
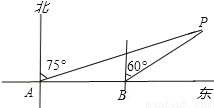
ij�ִ��������У���A�����С��P�ķ�λ�DZ�ƫ��75�㣬�ּ�������7�������B�����С��P�ķ�λ�DZ�ƫ��60�㣬���ʱ�ִ���С��P�ľ���BP= ���
 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭�����³�������·ʵ��ѧУ2017-2018ѧ�����꼶��ѧ��������ѧ�Ծ� ���ͣ������
��֪ ��
��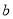 Ϊ����������������ʽ
Ϊ����������������ʽ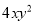 ��
�� 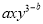 ��
�� 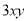 ��ӵõ��ĺ���Ȼ�ǵ���ʽ����ô
��ӵõ��ĺ���Ȼ�ǵ���ʽ����ô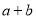 ��ֵ�����Ƕ��٣�����˵�����ɣ�
��ֵ�����Ƕ��٣�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2017-2018ѧ����̰�8�꼶����ѧ��ĩ��ϰ ���ͣ������
��֪��ֱ��y=x+1������B��2��n��������x�ύ�ڵ�A.
(1)��n����A����.
(2) ����P��x����һ��,�ҡ�APB�����Ϊ6,���P������.
��1��3����-1��0������2����3��0����-5��0���� �������������������1����B���������y=x+1�������n��ֵ����y=0��֪x=-1���Ӷ�ȷ����A���ꣻ ��2������P����x�������������IJ�ͬ�����÷���ķ������������P������꣮ ���������(1)��B��2��n����ֱ��y=x+1�� ��n=3 ��y=0����x=-1, ���A����Ϊ��-1��0���� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ������2017-2018ѧ����̰�8�꼶����ѧ��ĩ��ϰ ���ͣ���ѡ��
һ�κ���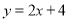 ��ͼ����y�ύ��������ǣ� ��
��ͼ����y�ύ��������ǣ� ��
A. ��0��-4�� B. ��0��4�� C. ��2��0�� D. ��-2��0��
B ��������������������ݵ���ֱ���ϵ���������㷽�̵Ĺ�ϵ���ڽ���ʽ����x=0�����������y��Ľ���������꣺ ��x=0����y=2��0+4=4��������y��Ľ��������ǣ�0��4���� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���½�������ʮ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
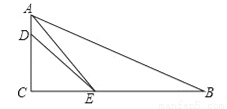
��֪��ͼ����Rt��ABC�У���ACB=90�㣬AEƽ�֡�BAC��BC�ڵ�E��DΪAC�ϵĵ㣬BE=DE��
��1����֤����B+��EDA=180�㣻
��2����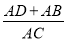 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���½�������ʮ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
����������һ���ϵĸ�����һ���ļн�Ϊ36�㣬��õ��������εĵǵĶ����� ��
63��� 27�㣮 �������� ������������������η�Ϊ��������κͶ۽�������������������õ��������ε����ʺ��������ڽǺͶ�������������ĵǵĶ����� ���У���,�ڣ� ?������������Σ�,��; ?�Ƕ۽������Σ�,�ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���½�������ʮ����2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�������������߳��ֱ���3��8���������ܳ��ǣ�������
A. 14 B. 19 C. 11 D. 14��19
B ������������3����������һ��Ҳ��3������8������3+3��8���ʲ����������Σ���ȥ�� ����3�ǵף�������8��8�� 3+8��8������������������ ���ܳ�Ϊ��3+8+8=19�� ��ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��������2017-2018ѧ���һѧ�ھ��꼶��ѧ��ĩ�����Ծ� ���ͣ������
��֪������y��x2��2mx��4 ��m>0���Ķ���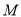 ��������ԭ��
��������ԭ��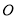 �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ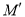 ������
������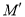 �������������ϣ����M������Ϊ_________��
�������������ϣ����M������Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ɽ��������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
�ک�1����2��0��1�ĸ�������С�����ǣ�������
A. ��1 B. ��2 C. 0 D. 1
B ���������ߡ� ��-1>-2�� ��-2<-1<0<1, ����С������-2. ��ѡB.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com