练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

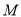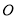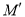    已知抛物线y＝x2－2mx－4 （m>0）的顶点关于坐标原点的对称点为．若点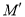在这条抛物线上，则点M的坐标为_________．

    (2,-8) 【解析】试题解析： 关于坐标原点的对称点为， 点在这条抛物线上， 解得： 故答案为：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型：填空题

    用科学记数法表示0.002 18=_______________．

    2.18×10-3 【解析】试题解析： 用科学记数法表示为： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：新疆阿克苏十二中2017-2018学年八年级（上）期中数学试卷 题型：填空题

    某轮船由西向东航行，在A处测得小岛P的方位是北偏东75°，又继续航行7海里后，在B处测得小岛P的方位是北偏东60°，则此时轮船与小岛P的距离BP= 海里．

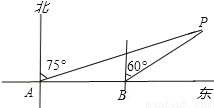
    7 【解析】 试题分析：过P作AB的垂线PD，在直角△BPD中可以求的∠PAD的度数是30度，即可证明△APB是等腰三角形，即可求解． 【解析】 过P作PD⊥AB于点D． ∵∠PBD=90°﹣60°=30° 且∠PBD=∠PAB+∠APB，∠PAB=90﹣75=15° ∴∠PAB=∠APB ∴BP=AB=7（海里） 故答案是：7．

    查看答案和解析>>

    科目：初中数学 来源：新疆阿克苏十二中2017-2018学年八年级（上）期中数学试卷 题型：单选题

    以下永洁环保、绿色食品、节能、绿色环保四个标志中，是轴对称图形是（　 　 ）

    A. B. C. D.

    B 【解析】试题分析：据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．可知：A、C、D不是轴对称图形，不符合题意；B、是轴对称图形，符合题意． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型：解答题

    某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图．根据图中提供的信息，解答下列问题：

    （1）补全频数分布直方图；

    （2）求扇形统计图中m的值和“E”组对应的圆心角度数；

    （3）请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数．

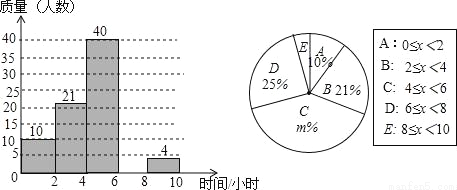
    （2）14．4°（3）870 【解析】试题分析：（1）根据A或B的人数与所占的百分数可求出总的，再求根据D组得百分比求得D组得人数，然后补全条形统计图； （2）用C的人数除以总人数，求得m的值，用E的人数除以总人数，再乘以360°即可求出扇形的度数； （3）找出不小于6的组别是D、E组，然后用二者的百分数的和乘以总人数即可． 试题解析：（1）补全频数分布直方图，如图所示． ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型：填空题

    花粉的质量很小，一粒某种植物花粉的质量约为0.000037mg，已知1g＝1000mg，那么0.000037mg可以用科学记数法表示为______________g．

    3.7×10-8 【解析】试题解析：0.000037mg用科学记数法表示为 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市区2017-2018学年第一学期九年级数学期末考试试卷 题型：单选题

    已知M=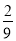a﹣1，N=a2﹣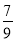a（a为任意实数），则M、N的大小关系为（ ）

    A. M＜N B. M=N C. M＞N D. 不能确定

    A 【解析】试题解析： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省鞍山市铁西区2017-2018学年七年级（上）期中数学试卷 题型：填空题

    单项式﹣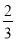xy2的系数是_____．

    【解析】∵单项式中的数字因数叫单项式的系数； ∴单项式﹣xy2的系数是.

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市番禺区2018届九年级上学期期末考试数学试卷 题型：解答题

    “国庆”期间，某电影院装修后重新开业，试营业期间统计发现，影院每天售出的电影票张数y（张）与电影票售价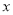（元/张）之间满足一次函数关系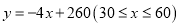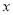： ， 是整数，影院每天运营成本为1600元，设影院每天的利润为w（元）（利润=票房收入运营成本）．

    （1）试求w与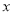之间的函数关系式；

    （2）影院将电影票售价定为多少时，每天获利最大？最大利润是多少元？

    （1）；（2）32元，最大利润是2624元． 【解析】试题分析：（1）根据“利润＝票房收入－运营成本”可得函数解析式； （2）将函数解析式配方成顶点式，由30≤x≤60，且x是整数结合二次函数的性质求解可得． 试题解析： 解:（1）由题意： ， 得w与之间的函数关系式为： . （2）， . 是整数, , 当或33时，w取得最大值，最大值为...

    查看答案和解析>>

    同步练习册答案