

分析 (1)先由AE=EC、BE=ED可判定四边形为平行四边形,再根据∠AEB=90°可判定该平行四边形为菱形;
(2)①连结OF,由切线可得OF为△ABD的高且OF=4,从而可得S△ABD,由OE为△ABD的中位线可得S△OBE=$\frac{1}{4}$S△ABD;
②作DH⊥AB于点H,结合①可知四边形OHDF为矩形,即DH=OF=4,根据sin∠DAB=$\frac{DH}{AD}$=$\frac{1}{2}$知∠EOB=∠DAH=30°,即∠AOE=150°,根据弧长公式可得答案
解答 解:(1)∵AE=EC,BE=ED,
∴四边形ABCD是平行四边形.
∵AB为直径,且过点E,
∴∠AEB=90°,即AC⊥BD.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
(2)①连结OF.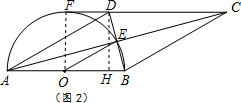
∵CD的延长线与半圆相切于点F,
∴OF⊥CF.
∵FC∥AB,
∴OF即为△ABD中AB边上的高.
∴S△ABD=$\frac{1}{2}$AB×OF=$\frac{1}{2}$×8×4=16,
∵点O是AB中点,点E是BD的中点,
∴S△OBE=$\frac{1}{4}$S△ABD=4.
②过点D作DH⊥AB于点H.
∵AB∥CD,OF⊥CF,
∴FO⊥AB,
∴∠F=∠FOB=∠DHO=90°.
∴四边形OHDF为矩形,即DH=OF=4.
∵在Rt△DAH中,sin∠DAB=$\frac{DH}{AD}$=$\frac{1}{2}$,
∴∠DAH=30°.
∵点O,E分别为AB,BD中点,
∴OE∥AD,
∴∠EOB=∠DAH=30°.
∴∠AOE=180°-∠EOB=150°.
∴弧AE的长=$\frac{150π×4}{180}$=$\frac{10}{3}π$.
点评 本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.


科目:初中数学 来源: 题型:选择题
| 年龄/岁 | 13 | 14 | 15 | 16 |
| 频数 | 5 | 15 | x | 10-x |
| A. | 平均数、中位数 | B. | 众数、中位数 | C. | 平均数、方差 | D. | 中位数、方差 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
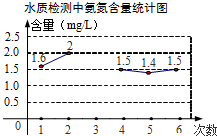 为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.
为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是1mg/L.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.845×1010元 | B. | 84.5×108元 | C. | 8.45×109元 | D. | 8.45×1010元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )| A. | 4S1 | B. | 4S2 | C. | 4S2+S3 | D. | 3S1+4S3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x-$\frac{5}{2}$)2-$\frac{11}{4}$ | B. | y=-(x+$\frac{5}{2}$)2-$\frac{11}{4}$ | C. | y=-(x-$\frac{5}{2}$)2-$\frac{1}{4}$ | D. | y=-(x+$\frac{5}{2}$)2+$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:
如图,△ABC中,∠A=60°,∠B=58°.甲、乙两人想在△ABC外部取一点D,使得△ABC与△DCB全等,其作法如下:| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com