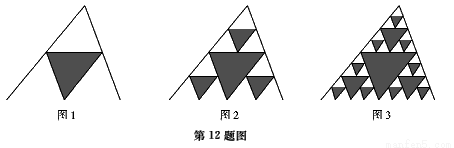
观察下列图形，它是把一个三角形分别连接这个三角形的中点，构成4个小三角形，挖去中间的小三角形（如题1）；对剩下的三角形再分别重复以上做法，……，将这种做法继续下去（如图2，图3……），则图6中挖去三角形的个数为（ ）
A．121 B．362 C．364 D．729
作业辅导系列答案科目：初中数学 来源：2017年初中毕业升学考试（山东日照卷）数学（解析版） 题型：选择题
已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：
①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（ ）
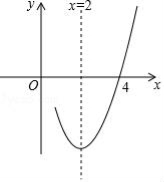
A．①②③ B．③④⑤ C．①②④ D．①④⑤
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（山东德州卷）数学（解析版） 题型：解答题
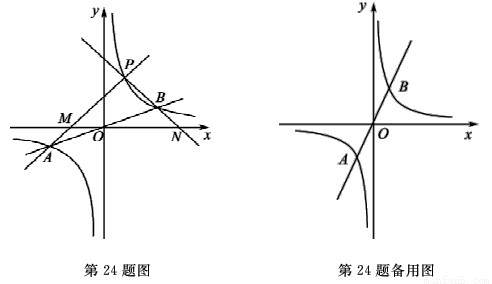
有这样一个问题：探究同一坐标系中系数互为倒数的正、反比例函数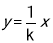
与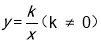
的图象性质.小明根据学习函数的经验，对函数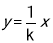与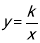
，当k>0时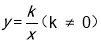的图象性质进行了探究，下面是小明的探究过程：
（1）如图所示，设函数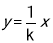与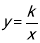图像的交点为A,B.已知A的坐标为(-k，-1)，则B点的坐标为 .
(2)若P点为第一象限内双曲线上不同于点B的任意一点.
①设直线PA交x轴于点M，直线PB交x轴于点N.求证：PM=PN.
证明过程如下：设P(m，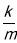
)，直线PA的解析式为y=ax+b(a≠0).
则
解得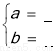
所以,直线PA的解析式为 ．
请把上面的解答过程补充完整，并完成剩余的证明.
②当P点坐标为(1,k)(k≠1)时，判断ΔPAB的形状，并用k表示出ΔPAB的面积.
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（山东德州卷）数学（解析版） 题型：填空题
某景区修建一栋复古建筑，其窗户设计如图所示.圆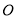
的圆心与矩形
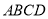对角线的交点重合，且圆与矩形上下两边相切（
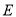为上切点），与左右两边相交(
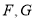为其中两个交点)，图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为
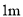，根据设计要求，若
，则此窗户的透光率（透光区域与矩形窗面的面枳的比值）为 ．
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（山东德州卷）数学（解析版） 题型：选择题
某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：
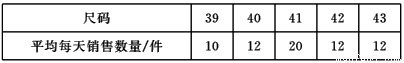
该店主决定本周进货时，增加一些41码的衬衫，影响该店主决策的统计量是（ ）
A．平均数 B．方差 C．众数 D．中位数
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（上海卷）数学（解析版） 题型：解答题
已知在平面直角坐标系xOy中（如图），已知抛物线y=﹣x2+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．
（1）求这条抛物线的表达式和点B的坐标；
（2）点M在对称轴上，且位于顶点上方，设它的纵坐标为m，联结AM，用含m的代数式表示∠AMB的余切值；
（3）将该抛物线向上或向下平移，使得新抛物线的顶点C在x轴上．原抛物线上一点P平移后的对应点为点Q，如果OP=OQ，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源：2017年初中毕业升学考试（山西卷）数学（解析版） 题型：填空题
如图，创新小组要测量公园内一棵树的高度AB，其中一名小组成员站在距离树10米的点E处，测得树顶A的仰角为54°．已知测角仪的架高CE=1.5米，则这颗树的高度为 米（结果保留一位小数．参考数据：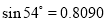
，
，
）．
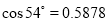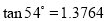查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是
的边
的中点，连接
并延长交
的延长线于
，若
，求
的长.