
��2017•���ޣ�������չ����ij���ĸ�ʱ��ν���������ͳ�����£�����������仯���ʱ���Ϊ����
9��00�C10��00 | 10��00�C11��00 | 14��00�C15��00 | 15��00�C16��00 | |
�������� | 50 | 24 | 55 | 32 |
�������� | 30 | 65 | 28 | 45 |
A. 9��00�C10��00 B. 10��00�C11��00 C. 14��00�C15��00 D. 15��00�C16��00
B �������������������ͳ�Ʊ��ɵã�10��00��11��00������24�ˣ�����65�ˣ���֮��� ��ѡ��B��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����Ĵ����ص�����ѧ���꼶�ڶ��ν��Կ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ�е�һ��������ͼ�ε�ƽ�ơ���ԳƼ���ת�ȱ任����,��������С�?������ͼ��Ӧ��(����)
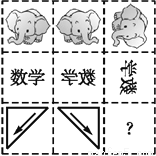
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ�����У2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У���P���C2��x2+1�����ڵ������ǣ� ��
A. ��һ���� B. �ڶ����� C. �������� D. ��������
B �������������������x2��0�� ��x2+1��1�� ���P��-2��x2+1���ڵڶ����ޣ� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��6.1���ݵ��ռ� ͬ����ϰ ���ͣ������
��������2012������������ˮ�ѵ�֧�������
��һ����ƽ��ÿ�� | �ڶ�����ƽ��ÿ�� | ��������ƽ��ÿ�� | ���ļ���ƽ��ÿ�� |
17Ԫ | 15Ԫ | 22Ԫ | 16Ԫ |
��1���������ȱȵڶ����ȶˮ�Ѷ���Ԫ��
��2����������2012������������ˮ�ѵ�֧�����ƶ���Ԫ��
��3����������2012��ƽ��ÿ������ˮ�ѵ�֧���Ƕ���Ԫ��
��1��7����2��70����3��17.5Ԫ. �������������������1���������ȵ�ˮ�����������ô𰸣� ��2���ĸ�������Ӽ����������֧�����ã� ��3�����ƽ�������ɣ� �����������1���������ȱȵڶ����ȶ�֧��22��15=7Ԫ�� ��2����֧��Ϊ17+15+22+16=70Ԫ�� ��3��ƽ��֧��Ϊ��70��4=17.5Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��6.1���ݵ��ռ� ͬ����ϰ ���ͣ������
Ϊ���˽�����6999�����꼶ѧ�����������������������ѧ��ͳ��֪ʶ���������������Ҫ�����ļ�����Ҫ�����������
���ռ����ݣ�����Ƶ����ʾ������������������壻�ܷ������ݣ����������ݣ�
����ȷ������Ϊ______��������ţ�
�ڢ٢ݢܢۣ� �������������������Ҫ�����ļ�����Ҫ�����������Ϊ�� ����Ƶ����ʾ������ռ����ݣ����������ݣ��ܷ������ݣ����������������壬 �ʴ�Ϊ���ڢ٢ݢܢۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��6.1���ݵ��ռ� ͬ����ϰ ���ͣ���ѡ��
�����ȡ���ݵķ�������ȷ���ǣ�������
A. ���ǰ�ͬѧ�������ò�������
B. ����˽���ʷ��������ù۲췽��
C. ��Ӳ�ҿ�������Ĵ�����ʵ�鷽��
D. ȫ��ͬѧ��ϲ����������÷��ʷ���
B ��������A.���ǰ�ͬѧ�������ò������������ŶȱȽϸߣ�B.����˽���ʷ��������ù۲췽�������ŶȺܵͣ�C.��Ӳ�ҿ�������Ĵ�����ʵ�鷽�������ŶȺܸߣ�D.ȫ��ͬѧ��ϲ����������÷��ʷ��������ŶȺܸߣ� ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.2.3����ԭ��ԳƵĵ������ ��ϰ ���ͣ������
��֪������y=x2-2x-3����ԭ��ԳƵ������ߵĽ���ʽΪ____.
y=-x2-2x+3. ���������������������ԭ��ԳƵ��������κ����������������ԭ��Գƣ����ڷ���ı䣮��ԭ���κ����Ľ���ʽΪ�� ����Գƺ�Ľ���ʽΪ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�1������ ���ͣ������
��ͼ��ʾ�����κ���y=-x2+2x+m��ͼ����x���һ������ΪA��3��0������һ������ΪB������y�ύ�ڵ�C��
��1����m��ֵ��
��2�����B�����ꣻ
��3���ö��κ���ͼ������һ��D��x��y��������x��0��y��0����ʹS��ABD=S��ABC�����D�����꣮
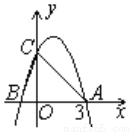
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����˽̰���ѧ���꼶�ϲ� ��23�� ��ת ȫ�²��Ծ� ���ͣ���ѡ��
��ͼ����֪�۽�������ABC������ABC�Ƶ�A����ʱ�뷽����ת110��õ���AB��C�䣬����BB�䣬��AC���BB�䣬���CAB��Ķ���Ϊ��������
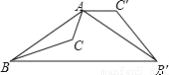
A. 55�� B. 65�� C. 75�� D. 85��
C ���������������������õ������������ʣ���ת�����ʺ�ƽ���ߵ����ʼ������. ����������ת֪��AB=A B��,��BA B��=110��,���AB B��=��A B��B=35�� ����AC���BB�� ���C��A B��=��A B��B=35�㣬���BAC=35�㣬���CAB��=75��. ��ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com