
当m为何值时,一元二次方程(m2-1)x2+2(m-1)x+1=0:
(1)有两个不相等的实数根;
(2)有两个相等的实数根;
(3)没有实数根.
(1) m>1且m≠-1;(2) 原方程不可能有两个相等的实数根;(3) m>1时原方程没有实数根. 【解析】试题分析:需要先求m2-1 ,(1)判别式大于0.(2)判别式等于0.(3)判别式小于0. 试题解析: (1) m2-1 ,m, ∵Δ= ∴m>1且m≠-1 (2)∵Δ= ∴m=1 ∵ ∴m≠1 ∴原方程不可能有两个相等的实数根. (3)当Δ... 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源:黑龙江省2017-2018学年九年级数学上学期期末试卷 题型:解答题
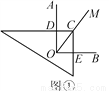
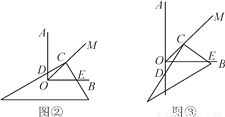
已知∠AOB=90°,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA,OB(或它们的反向延长线)相交于点D,E.
当三角板绕点C旋转到CD与OA垂直时(如图①),易证:OD+OE=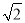 OC;
OC;
当三角板绕点C旋转到CD与OA不垂直时,即在图②,图③这两种情况下,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段OD,OE,OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级上学期期末模拟数学试卷 题型:单选题
如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为( )
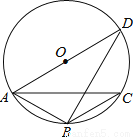
A. 3 B. 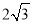 C. 3
C. 3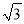 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:江西省上饶市2017届九年级(上)期末数学试卷(解析版) 题型:填空题
在如图所示的网格中,每个小正方形的边长都为1,若以小正形的顶点为圆心,2为半径作一个扇形围成一个圆锥,则所围成的圆锥的底面圆的半径为______.
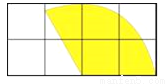
查看答案和解析>>
科目:初中数学 来源:江西省上饶市2017届九年级(上)期末数学试卷(解析版) 题型:单选题
在下列图形中,是中心对称图形而不是轴对称图形的是( )
A. 圆 B. 等边三角形 C. 梯形 D. 平行四边形
D 【解析】【解析】 选项A、是中心对称图形,也是轴对称图形,故此选项错误; 选项B、不是中心对称图形,是轴对称图形,故此选项错误; 选项C、不是中心对称图形,是轴对称图形,故此选项错误; 选项D、是中心对称图形,不是轴对称图形,故此选项正确; 故选D.查看答案和解析>>
科目:初中数学 来源:北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型:填空题
某商品经过连续两次降价,销售单价由原来的125元降到80元,则平均每次降价的百分率为_____.
20% 【解析】试题分析:设这种商品平均每次降价的百分率为x,根据题意列方程得, 125(1-x)2=80, 解得x1=0.2=20%,x2=1.8(不合题意,舍去);查看答案和解析>>
科目:初中数学 来源:北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型:单选题
配方法解方程2x2-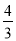 x-2=0变形正确的是 ( )
x-2=0变形正确的是 ( )
A. (x- )2=
)2= B. (x-
B. (x- )2=0
)2=0
C. (x+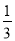 )2=
)2=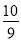 D. (x-
D. (x-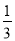 )2=
)2=
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测题 题型:填空题
如图所示,正方形ABCD的边长是2,以正方形ABCD的边AB为边,在正方形内作等边三角形ABE,P为对角线AC上的一点,则PD+PE的最小值为____
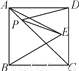
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形并证明.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你作出判断,说明理由.
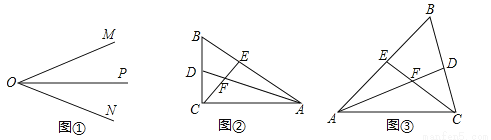
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com