练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某商品经过连续两次降价，销售单价由原来的125元降到80元，则平均每次降价的百分率为_____．

    20% 【解析】试题分析：设这种商品平均每次降价的百分率为x，根据题意列方程得， 125（1-x）2=80， 解得x1=0.2=20%，x2=1.8（不合题意，舍去）；
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黑龙江省2017-2018学年九年级数学上学期期末试卷 题型：解答题

    如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，4），B（4，2），C（3，5）（每个方格的边长均为1个单位长度）．

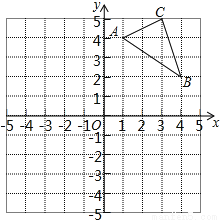
    （1）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A1B1C1；

    （2）求出点B旋转到点B1所经过的路径长．

    （1）见解析；（2）π． 【解析】 试题分析：（1）根据旋转的性质，可得答案； （2）根据线段旋转，可得圆弧，根据弧长公式，可得答案． 【解析】 （1）如图： ； （2）如图2： ， OB==2， 点B旋转到点B1所经过的路径长=π．

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：解答题

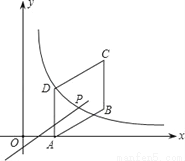
    如图，四边形ABCD是平行四边形，点A（1，0），B（4，1），C（4，3），反比例函数y=的图象经过点D，点P是一次函数y=mx+3﹣4m（m≠0）的图象与该反比例函数图象的一个公共点；

    （1）求反比例函数的解析式；

    （2）通过计算说明一次函数y=mx+3﹣4m的图象一定过点C；

    （3）对于一次函数y=mx+3﹣4m（m≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围，（不必写过程）

    （1）y=；（2）C（4，3）；（3）见解析. 【解析】试题分析：（1）由B（4，1），C（4，3）得到BC⊥x轴，BC=2，根据平行四边形的性质得AD=BC=2，而A点坐标为（1，0），可得到点D的坐标为（1，2），然后把D（1，2）代入y=即可得到k=2，从而可确定反比例函数的解析式； （2）把x=4代入y=mx+3﹣4m（m≠0）得到y=3，即可说明一次函数y=mx+3﹣4m（m≠0...

    查看答案和解析>>

    科目：初中数学 来源：江西省上饶市2017届九年级（上）期末数学试卷（解析版） 题型：单选题

    如图，不能判定△AOB和△DOC相似的条件是（　　）

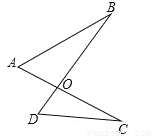
    A. AO•CO=BO•DO B. 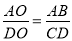C. ∠A=∠D D. ∠B=∠C

    B 【解析】选项A、能判定．利用两边成比例夹角相等． 选项B、不能判定． 选项C、能判定．利用两角对应相等的两个三角形相似． 选项D、能判定．利用两角对应相等的两个三角形相似． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：解答题

    当m为何值时，一元二次方程(m2－1)x2＋2(m－1)x＋1＝0：

    (1)有两个不相等的实数根；

    (2)有两个相等的实数根；

    (3)没有实数根．

    (1) m>1且m≠-1;(2) 原方程不可能有两个相等的实数根;(3) m>1时原方程没有实数根. 【解析】试题分析：需要先求m2－1 ，(1)判别式大于0.(2)判别式等于0.（3）判别式小于0. 试题解析： (1) m2－1 ,m, ∵Δ= ∴m>1且m≠-1 (2)∵Δ= ∴m=1 ∵ ∴m≠1 ∴原方程不可能有两个相等的实数根. （3）当Δ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：单选题

    三角形两边的长分别是3和6，第三边的长是方程x2－6x＋8＝0的解，则这个三角形的周长是 (　　)

    A. 11 B. 13

    C. 11或13 D. 不确定

    B 【解析】试题分析：方程的解为x1=2，x2=4，可得根据三角形的三边关系可得，只有4才能是这个三角形的第三边，所以这个三角形的周长是13，故答案选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上数学第二章《一元二次方程》单元检测卷 题型：单选题

    已知关于x的方程x2＋bx＋a＝0有一个根是－a(a≠0)，则下列代数式的值恒为常数的是 (　　)

    A. ab B. 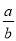C. a＋b D. a－b

    D 【解析】－a代入方程， , , , . 所以选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（华师大版）：期末检测题 题型：填空题

    计算：()－1－＝____．

    0 【解析】原式=2-2=0. 故答案为：0.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上学期第二次月考数学试卷 题型：解答题

    （1）化简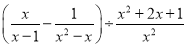： ，并从﹣1，0，1，2中选择一个合适的数求代数式的值．

    （2）已知x2＋y2＋6x－4y＋13=0，求 ．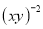

    （1）， ；（2）． 【解析】试题分析：（1）根据分式的混合运算的法则，通分，把除法化为乘法，完成约分化简，然后代入分母不为0的数（x≠±1，0）代入求值即可. （2）根据配方法和非负数的意义，直接变形，求出x、y的值，再代入求解即可. 试题解析：（1） = = = = 当x=2时，原式=. （2）∵x2＋y2＋6x－4y＋13=0 ∴x...

    查看答案和解析>>

    同步练习册答案