
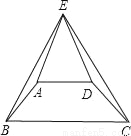
已知如图,等腰梯形ABCD,AB=CD,BE=CE,求证:AE=DE.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型:解答题
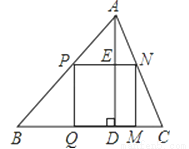
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型:单选题
在△ABC中,若|sinA﹣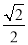 |+(
|+(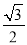 ﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
﹣cosB)2=0,∠A,∠B都是锐角,则∠C的度数是( )
A. 75° B. 90° C. 105° D. 120°
C 【解析】【解析】 ∵|sinA﹣|=0,( ﹣cosB)2=0,∴sinA﹣=0, ﹣cosB=0,∴sinA=, =cosB,∴∠A=45°,∠B=30°,∴∠C=180°﹣∠A﹣∠B=105°.故选C.查看答案和解析>>
科目:初中数学 来源:安徽省宿州市(城西校区) 2017-2018学年九年级第一学期期中测试数学试卷 题型:单选题
为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
A. 289(1-x)2=256
B. 256(1-x)2=289
C. 289(1-2x)=256
D. 256(1-2x)=289
A 【解析】 试题分析:第一次降价后的价格为289(1-x),第一次降价后的价格为289(1-x)(1-x),即289(1-x)2=256; 故选A.查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:解答题
市政公司为绿化建设路风景带,计划购买甲乙两种树苗600株,甲种树苗每株50元,乙种树苗每株70元.有关统计表明,甲乙两种树苗的成活率分别为80%和95%.(注:成活率= ×100%).
×100%).
(1)若购买树苗的钱不超过40000元,应如何选购甲、乙两种树苗;
(2)若希望这批树苗的成活率不低于90%,且购买树苗的费用最低,应如何选购甲、乙两种树苗并求出最低费用是多少元.
(1)选购甲种树苗不少于100株,乙种树苗不超过500株;(2)购买甲种树苗200株,乙种树苗400株时费用最低,最低费用是38000元. 【解析】【试题分析】 (1)根据总费用,列出不等式即可.设选购甲种树苗x株,则选购乙种树苗为(600﹣x)株,根据题意得,50x+70(600﹣x)≤40000,解得x≥100,即选购甲种树苗不少于100株,乙种树苗不超过500株. (2)设...查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:填空题
人民公园的侧门口有9级台阶,小聪一步只能上1级台阶或2级台阶,小聪发现当台阶数分别为1级、2级、3级、4级、5级、6级、7级……逐渐增加时,上台阶的不同方法的种数依次为1、2、3、5、8、13、21……这就是著名的斐波那契数列.那么小聪上这9级台阶共有 种不同方法
55查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学三模试卷 题型:单选题
中央电视台“幸运52”栏目中有“砸金蛋”互动环节.游戏规则如下:在20个金蛋中,若砸开后,金花四射,则为中奖,否则就不得奖,其中有15个金蛋砸开后“金花四射”.某次共有3名观众参与砸蛋,前两名观众砸开金蛋后均未出现金花四射,则第三名观众砸开金蛋后,不得奖的概率为( )
A. 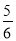 B.
B. 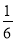 C.
C. 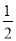 D.
D. 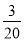
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:单选题
如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为_____.
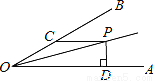
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:解答题
已知x=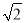 +1,求x+1﹣
+1,求x+1﹣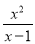 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com