
如图,在平行四边形ABCD中,点E在边DC上,联结AE并延长交BC的延长线于点F,若AD=3CF,那么下列结论中正确的是( )
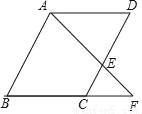
A. FC:FB=1:3 B. CE:CD=1:3 C. CE:AB=1:4 D. AE:AF=1:2.
C 【解析】试题解析:∵四边形ABCD是平行四边形, ∴AD∥BC,AD=BC,AB=DC ∴△ADE∽△FCE ∴AD:FC=AE:FE=DE:CE ∵AD=3FC ∴AD:FC=3:1 ∴FC:FB=1:4,故A错误; ∴CE:CD=1:4,故B错误; ∴CE:AB=CE:CD=1:4,故C正确; ∴AE:AF=3:4,故D错误. ... 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:解答题
规定两数a,b之间的一种运算,记作(a,b):如果 ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:(3,27)=_______,(5,1)=_______,(2,  )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n,
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
(1)3,0,-2;(2)(3,20) 【解析】试题分析:(1)根据新定义的运算即可得; (2)设(3,4)=x,(3,5)=y,由定义则有, =5,由同底数幂的乘法可得,从而有(3,20)=x+y ,所以(3,4)+(3,5)=(3,20) 试题解析:(1)∵33=27,50=1,2-2= ,∴(3,27)=3,(5,1)=0,(2, )=-2. 故答案依次为:3,0,-...查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:单选题
在下列图形中,线段PQ的长度表示点P到直线L的距离的是( )
A.  B.
B. 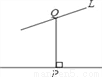 C.
C. 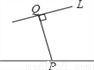 D.
D. 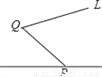
查看答案和解析>>
科目:初中数学 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
已知弓形的高是1厘米,弓形的半径长是13厘米,那么弓形的弦长是_____厘米.
10 【解析】试题解析:如图, 过圆心O作OD⊥AB,交弧于C.则CD=1,连接OA. 在直角△AOD中,OA=13,OD=13-CD=12, 则AD==5, ∴AB=2AD=10. 故答案是:10.查看答案和解析>>
科目:初中数学 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:填空题
如果函数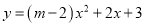 (
(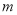 为常数)是二次函数,那么
为常数)是二次函数,那么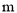 取值范围是 ____.
取值范围是 ____.
查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:解答题
某服装柜在销售中发现:其专柜某款童装平均每天可售出 20 件,每件盈利 40 元。为了迎接“元旦”,商场决定采取适当的降价措施,扩大销售量,增加盈利。经市场调查发现:如果每件 童装降价 1 元,那么平均每天就可多售出 2 件。要想平均每天销售这种童装上盈利 1200 元,又能尽量 减少库存,那么每件童装应降价多少元?
每件童装应降价 20 元 【解析】试题分析:设每件童装应降价x元,则每件童装实际盈利(40﹣x)元.根据利润=单件利润×销售数量即可得出关于x的一元二次方程,解之即可得出x的值,为了减少库存,取其较大值即可. 试题解析:【解析】 设每件童装应降价x元,则每件童装实际盈利(40﹣x)元.由题意可得: (40﹣x)(20+2x)=1200,整理得:x2﹣30x+200=0,解得:x...查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:填空题
某种药品经过两次降价由原来的每盒 12.5 元降到每盒 8 元,如果 2 次降价的百分率相同,设每次降价的百分率为 x,可列出的方程为_____.
12.5(1-x)2=8 【解析】【解析】 根据题意得:12.5(1﹣x)2=8.故答案为:12.5(1﹣x)2=8.查看答案和解析>>
科目:初中数学 来源:2017-2018学年人教版八年级数学下册:期中测评 题型:解答题
已知a,b为一个等腰三角形的两条边长,并满足b=2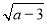 +
+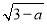 +5,求此等腰三角形的周长.
+5,求此等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知:点O到△ABC的两边AB、AC所在直线的距离OD=OE,且OB=OC.
(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com