
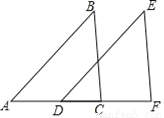
��֪AB��DE��BC��EF��D��C��AF�ϣ���AD=CF����֤����ABC�ա�DEF��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017���Ĵ�ʡ�п���ѧģ���Ծ���3�� ���ͣ������
���㣺cos245��+tan30��•sin60��= ��
1 �������� �����������cos45��=��tan30��=��sin60��=���뼴�ɵó��𰸣� �������� cos245��+tan30��•sin60��=+��==1�� �ʴ�Ϊ��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ������
��֪��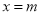 ��
��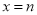 ʱ������ʽ
ʱ������ʽ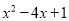 ��ֵ��ȣ���
��ֵ��ȣ���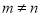 ����
����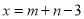 ʱ����ʽ
ʱ����ʽ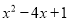 ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
��ͼ����A��B�ڷ���������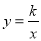 ��ͼ���ϣ�����A��B��x��Ĵ��ߣ�����ֱ���M��N������AB��x���ڵ�C����OM=MN=NC���ı���AMNB�������3����k��ֵΪ�� ��
��ͼ���ϣ�����A��B��x��Ĵ��ߣ�����ֱ���M��N������AB��x���ڵ�C����OM=MN=NC���ı���AMNB�������3����k��ֵΪ�� ��
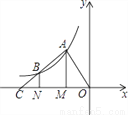
A. 2 B. 4 C. ��2 D. ��4
D ��������������������������������ʽ�õ�S��AOM=S��AOC��S��ACM=4S��BCN���ٸ��ݷ����������ı���ϵ��k�ļ�������õ�S��AOM=|k|��Ȼ������k��0ȥ����ֵ��⣮ �������� �ߵ�A��B�ڷ���������y��ͼ���ϣ� ��S��AOM=|k|�� ��OM=MN=NC�� ��AM=2BN�� ��S��AOM=S��AOC��S��ACM=4S��BCN��S��ACM=2...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С������ ���ͣ���ѡ��
����ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε���( )
A. 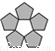 B.
B. 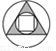 C.
C.  D.
D. 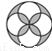
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
�ڵ���������ABC�У�AB=AC����AB�Ĵ�ֱƽ������AC���ڵ�ֱ���ཻ���ɵ����Ϊ50�㣬��������ABC�ĵ���_____��
70���20�� ��������������������ݡ�ABC�С�AΪ�����۽ǣ���Ϊ��������� �ٵ���AΪ���ʱ�� ��AB�Ĵ�ֱƽ������AC���ڵ�ֱ���ཻ���õ����Ϊ50�㣬 ���A=40�㣬 ���B=�� �ڵ���AΪ�۽�ʱ�� ��AB�Ĵ�ֱƽ������AC���ڵ�ֱ���ཻ���õ����Ϊ50�㣬 ���1=40�㣬 ���BAC=140�㣬 ���B=��C=�� ��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
һ��������ε�ÿ����Ƕ���36�㣬���������εı����ǣ�������
A. 9 B. 10 C. 11 D. 12
B �������������������Ϊ������εĵ���Ǻ͵���360�㣬��ÿ����Ƕ���36�㣬�������������εı���=360���36��=10����ѡ��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
4��10ʱ����������ɵĽǶ�Ϊ_____��
65�� �������������汻12��Сʱ�ֳ�12���ÿ1����Ӧ�Ķ���Ϊ30�㣬 �� 4������ʱ������ʱ��ļн�Ϊ120��. �ߴ�4������4��10���ڼ䣬����ת����2��ת��60�㣻ʱ��ת���˸�ת��5�㣬 ��4��10�ֵ�ʱ��ʱ�������ļн�Ϊ��120��+5��-60��=65��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD���ཻ�ڵ�O��EF����O����AB��CD�ֱ��ཻ�ڵ�E��F����֤��AE=CF��
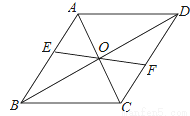
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com