
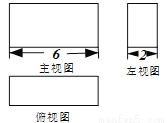
如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是______
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:解答题
指出变化过程中的变量与常量:
(1)y=﹣2πx+4;
(2)v=v0t+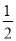 at(其中v0,a为定值);
at(其中v0,a为定值);
(3)n边形的对角线的条数l与边数n的关系是:l=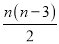 .
.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:单选题
下列计算中,正确的是 ( )
A. 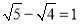 B.
B. 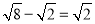 C.
C. 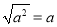 D.
D. 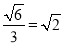
查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:解答题
如图,直线AB、CD、EF相交于一点O,∠AOD=3∠AOF,∠AOC=120°,求∠BOE的度数.
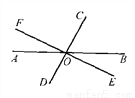
查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:填空题
已知直线a,b,c在同一平面内,给出下列说法:①如果a⊥b,b⊥c,那么a∥c;②如果a∥b,b∥c,那么a∥c;③如果a∥b,b⊥c,那么a⊥c;④如果a与b相交,b与c相交,那么a与c相交.在上述四种说法中,正确的有__________个.
3 【解析】①如果a⊥b,b⊥c,那么a∥c,正确; ②如果a∥b,b∥c,那么a∥c,正确; ③如果a∥b,b⊥c,那么a⊥c,正确; ④如果a与b相交,b与c相交,那么a与c相交,错误,a与c有可能平行. 故答案为3.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β-∠γ的值等于( )
A. 45° B. 60° C. 90° D. 180°
C 【解析】试题分析:根据互余两角之和为90°,互补两角之和为180°,结合题意即可得出答案. 【解析】 由题意得,∠α+∠β=180°,∠α+∠γ=90°, 两式相减可得:∠β﹣∠γ=90°. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018苏科版南京栖霞区七年级数学上册12月份月考试卷有答案 题型:单选题
下列图形中,沿其一边快速旋转能得到圆柱的是 ( )
A. 直角三角形 B. 梯形 C. 长方形 D. 等腰三角形
C 【解析】因为圆柱的上底圆和下底圆分别是两个半径相等的圆,所以是梯形. 故选C.查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
写出一个无解的一元一次不等式组为 ________.
. 【解析】【解析】 根据不等式组解集的口诀:大大小小找不到(无解),可写x≤2,x≥3,即. 故答案为: .查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学三模试卷 题型:填空题
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在_____.
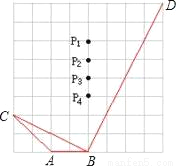
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com