
若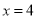 是关于
是关于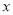 的方程
的方程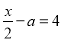 的解,则
的解,则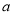 的值为( )
的值为( )
A. -6 B. 2 C. 16 D. -2
D 【解析】把代入方程得:2-a=4,解得:a=-2, 故选D. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:解答题
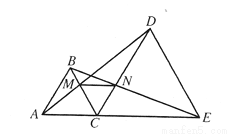
如图,C是线段AE上一点,△ABC、△CDE都是等边三角形,AD与BC交于点M,BE与CD交于点N。
试说明:(1)AD=BE;(2)MN//AE。
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:单选题
如图, 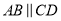 ,
, 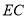 交
交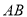 于点
于点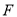 ,
, 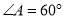 ,
, 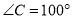 ,则
,则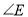 的大小为( ).
的大小为( ).
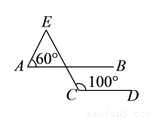
A. 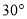 B.
B. 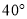 C.
C. 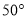 D.
D. 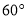
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年七年级上学期第二次六校联考数学试卷 题型:解答题
计算题:(1)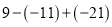 ;(2)
;(2)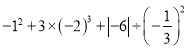
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年七年级上学期第二次六校联考数学试卷 题型:单选题
某个商贩同时卖出两件上衣,售价都是135元,按成本计算,其中一件盈利25%,另一件亏损25%,在这次交易中,该商贩( )
A. 不赔不赚 B. 赚9元 C. 赔9元 D. 赔18元
D 【解析】设在这次买卖中盈利那件衣服的原价x元,另一件的原价为y元, 则可列方程:(1+25%)x=135, 解得:x=108, 比较可知,第一件赚了27元, 第二件可列方程:(1-25%)y=135, 解得:x=180, 比较可知亏了45元, 两件相比则一共亏了18元, 故选C.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2017-2018学年七年级上学期第二次六校联考数学试卷 题型:单选题
2017年中秋、国庆假日八天里,中国民航共运送旅客1295万人次,将1295万用科学记数法表示应为( )
A. 0.1295 ?108 B. 1295?104 C. 12.95 ?106 D. 1.295?107
D 【解析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数, 1295万= 1.295?107, 故选D.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
已知:如图,∠CAE是△ABC的外角,∠1=∠2,AD∥BC,求证:△ABC是等腰三角形.
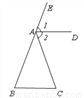
查看答案和解析>>
科目:初中数学 来源:内蒙古呼和浩特市土默特左旗2017-2018学年七年级(上)期中数学试卷 题型:解答题
有理数a、b、c在数轴上的位置如图所示,试化简:|a﹣c|﹣|a﹣b|+|b﹣c|.

查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2018届九年级上期末模拟数学试卷 题型:单选题
如图,点M在BC上,点N在AM上,CM=CN, 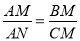 ,下列结论正确的是( )
,下列结论正确的是( )
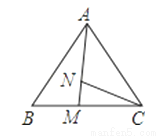
A. △ABM∽△ACB B. △ANC∽△AMB C. △ANC∽△ACM D. △CMN∽△BCA
B 【解析】∵CM=CN, ∴∠CNM=∠CMN, ∴180°-∠CMN=180°-∠CNM,即∠AMB=∠ANC, ∵CM=CN, , ∴ , ∴△AMB∽△ANC. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com