
解不等式组: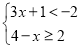
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源:广州市2018学年度七年级(上)数学期末测试卷 题型:单选题
如图所示,将一块直角三角板的直角顶点O放在直尺的一边CD上,如果∠AOC=27°24,32,,,那么∠BOD等于

A.70°24′32″ B.62°35′28″
C.52°44′38″ D.28°24′32″
B. 【解析】 试题分析:由题意得,∠AOC+∠AOB+∠BOD=180°, 解得:∠BOD=62°35′28″. 故选B.查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 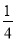 (-4x2+2x-8)-(
(-4x2+2x-8)-(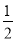 x-1),其中x=
x-1),其中x=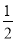 .
.
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
下列各式计算正确的是 ( )
A. 6a+a=6a2 B. -2a+5b=3ab C. 4m2n-2mn2=2mn D. 3ab2-5b2a=-2ab2
D 【解析】A. 6a+a=7a,故错误; B. -2a与5b不是同类项,不能合并,故错误; C. 4m2n与-2mn2不是同类项,不能合并,故错误;D. 3ab2-5b2a=-2ab2,正确;故选D .查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:解答题
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
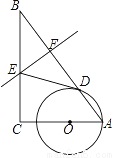
(1)求证:直线DE是⊙O的切线;
(2)若AC=6,BC=8,OA=2,求线段AD和DE的长.
(1)见解析;(2)4.75. 【解析】试题分析:(1)连接OD,通过线段垂直平分线的性质和等腰三角形的性质证明∠EDB+∠ODA=90°,进而得出OD⊥DE,根据切线的判定即可得出结论; (2)连接OE,作OH⊥AD于H.则AH=DH,由△AOH∽△ABC,可得,推出AH=,AD=,设DE=BE=x,CE=8-x,根据OE2=DE2+OD2=EC2+OC2,列出方程即可解决问题; ...查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:填空题
如图,以AB为直径,点O为圆心的半圆经过点C,若AC=BC=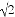 ,则图中阴影部分的面积是___________
,则图中阴影部分的面积是___________
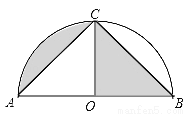
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:单选题
圆锥的底面半径为4cm,高为3cm,则它的表面积为( )
A. 12π cm2 B. 20π cm2 C. 26π cm2 D. 36π cm2
D 【解析】试题分析:底面周长是2×4π=8πcm,底面积是:42π=16πcm2. 母线长是: =5, 则圆锥的侧面积是: ×8π×5=20πcm2, 则圆锥的表面积为16π+20π=36πcm2. 故选D.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型:填空题
等腰三角形一腰上的高与另一腰的夹角为52º,则该三角形的底角的度数为________.
71°或19° 【解析】试题解析:分两种情况讨论: ①若∠A<90°,如图1所示: ∵BD⊥AC, ∴∠A+∠ABD=90°, ∵∠ABD=52°, ∴∠A=90°-52°=38°, ∵AB=AC, ∴∠ABC=∠C=(180°-38°)=71°; ②若∠A>90°,如图2所示: 同①可得:∠DAB=90°-52°=38°, ∴∠B...查看答案和解析>>
科目:初中数学 来源:2017年山东省枣庄市中考数学模拟试卷 题型:解答题
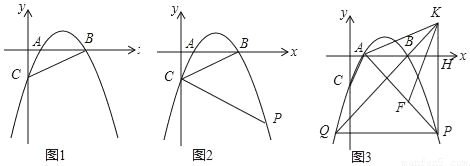
在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点且在直线BC下方,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4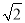 a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com