
(1)已知a,b,c均为实数,且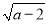 +|b+1|+(c+2)2=0,求关于x的方程ax2+bx+c=0的根;
+|b+1|+(c+2)2=0,求关于x的方程ax2+bx+c=0的根;
(2)已知二次函数y=ax2+bx+c的图象经过A(﹣1,0),B(0,﹣3),C(4,5)三点,求该二次函数的解析式.
(1)x1=,x2=;(2)抛物线解析式为y=x2﹣2x﹣3. 【解析】分析:(1)先根据算术平方根、绝对值、偶次方都大于等于0,可得三个非负数相加和为0,则这三个数的值必都为0,由此可解出a、b、c的值,再代入方程中求解. (2)把A、B、C三点的坐标分别代入y=ax2+bx+c得到关于a、b、c的方程组,然后解方程组求出a、b、c的值即可. 本题解析: (1)∵+|b+...科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
已知等腰三角形的周长为15cm,其中一边长为7 cm,则底边长为__________.
1 cm或7 cm 【解析】试题解析:当底为7cm时,此时腰长为4cm和4cm,满足三角形的三边关系; 当腰为7cm时,此时另一腰为7cm,则底为1cm,满足三角形的三边关系; 所以底边长为1cm或7cm.查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
如图,A、B两地之间有一座山,汽车原来从A地到B地经过C地沿折线A→C→B行驶,现开通隧道后,汽车直接沿直线AB行驶.已知AC=10千米,∠A=30°,∠B=45°.则隧道开通后,汽车从A地到B地比原来少走多少千米?(结果保留根号)
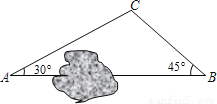
查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:单选题
点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-x2+2x+c的图象上,则y1,y2,y3的大小关系是( )
A. y3>y2>y1 B. y3>y1=y2 C. y1>y2>y3 D. y1=y2>y3
D 【解析】∵y=?x2+2x+c, ∴对称轴为x=1, P2(3,y2),P3(5,y3)在对称轴的右侧,y随x的增大而减小, ∵3<5, ∴y2>y3, 根据二次函数图象的对称性可知,P1(?1,y1)与(3,y1)关于对称轴对称, 故y1=y2>y3, 故选D.查看答案和解析>>
科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:解答题
某商场要经营一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
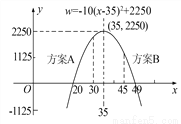
(1)写出商场销售这种工具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;
(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
(1)w=-10x2+700x-10000; (2)销售单价为35元时,每天销售利润最大,最大利润为2250元; (3)方案A的最大利润更高,理由见解析. 【解析】试题分析:(1)根据利润=(销售单价-进价)×销售量,列出函数关系式即可; (2)根据(1)式列出的函数关系式,运用配方法求最大值; (3)分别求出方案A、B中x的取值范围,然后分别求出A、B方案的最大利润...查看答案和解析>>
科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:填空题
若一元二次方程的x2﹣2x﹣3599=0两根为a,b,且a>b,则2a﹣b的值为_____.
181 【解析】x2﹣2x=3599, x2﹣2x+1=3600 (x﹣1)2=3600, x﹣1=±60, 所以a=61,b=﹣59, 所以2a﹣b=2×61﹣(﹣59)=181. 故答案为181.查看答案和解析>>
科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:单选题
方程x2+3x﹣6=0与x2﹣6x+3=0所有根的乘积等于( )
A. ﹣18 B. 18 C. ﹣3 D. 3
A 【解析】试题分析:由根与系数的关系可得:方程x2+3x-6=0的两根的乘积是-6,x2-6x+3=0的两根的乘积是3,所以方程x2+3x-6=0与x2-6x+3=0所有根的乘积=-6×3=-18,故选:A.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
已知点A、B、P在一条直线上,则下列等式中,能判断点P是线段AB的中点的个数有( )
①AP=BP; ②2BP=AB; ③AB=2AP; ④AP+PB=AB.
A. 1个 B. 2个 C. 3个 D. 4个
A 【解析】①当点P在线段AB上时,满足AP=BP的点P为线段AB的中点. 当点P不在线段AB上时,该等式不成立. 因此,满足AP=BP的点P为线段AB的中点. 故等式①符合题意. ②当点P在线段AB上时,满足2BP=AB的点P为线段AB的中点. 当点P不在线段AB上时,根据该等式可画出如下示意图. 因此,满足2BP=AB的点P不一定为线段AB的中点. ...查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
解方程:(1) 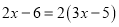 (2)
(2) 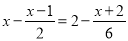
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com