
在Rt△ABC中,∠C=90°,AB=1,则AB2+BC2+AC2=__.
2 【解析】由勾股定理得,BC2+AC2=1,则AB2+BC2+AC2=2.科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(1)测试 题型:单选题
在一个近似直角三角形的空地上要挖一长方形的水池,要求长方形水池的两个边在直角三角形空地的直角边上,若测量出直角三角形的三边长分别为30m,40m,50m,则水池的最大面积可以为()
A. 300m2 B. 325m2 C. 400m2 D. 285m2
A 【解析】如图所示, 设DF=x,DE=y,在△ABC中,DF∥AB,可得,即, 同理可得,即, 由AD+CD=AC,可得: ,则矩形花园的面积, 当且仅当x=15,y=20时, ,则AD=CD=25,即点D为AC的中点时,矩形花园的面积最大,且为300,故选A.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:解答题
如图,一次函数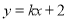 的图象与反比例函数
的图象与反比例函数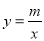 的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交
的图象交于点P,点P在第一象限.PA⊥x轴于点A,PB⊥y轴于点B.一次函数的图象分别交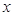 轴、
轴、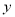 轴于点C、D,且S△PBD=4,
轴于点C、D,且S△PBD=4, 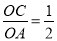 .
.
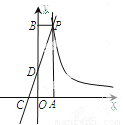
(1)求点D的坐标;
(2)求一次函数与反比例函数的解析式;
(3)根据图象写出当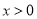 时,一次函数的值大于反比例函数的值的
时,一次函数的值大于反比例函数的值的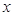 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为( )
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
C 【解析】试题分析:根据相似三角形面积的比等于相似比的平方计算即可得解.∵△ABC∽△A′B′C′,相似比为1:2,∴△ABC与△A′B′C′的面积的比为1:4. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
如图,铁路上A,B两点相距25km,C,D为两村庄,AD⊥AB于点A,BC⊥AB于点B,已知AD=15km,BC=10km,现在要在铁路AB旁建一个货运站E,使得C,D两村到E站距离相等,问E站应建在离A地多远的地方?
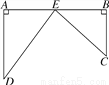
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
如图,所有三角形都是直角三角形,所有四边形都是正方形,已知S1=4,S2=9,S3=8,S4=10,则S=( )
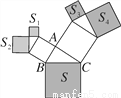
A. 25 B. 31 C. 32 D. 40
B 【解析】试题分析:如图,分别求出AB2、AC2,进而得到BC2,即可解决问题. 【解析】 如图,由题意得: AB2=S1+S2=13, AC2=S3+S4=18, ∴BC2=AB2+AC2=31, ∴S=BC2=31, 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A. 25 B. 14 C. 7 D. 7或25
D 【解析】试题分析:根据直角三角形的性质可得:第三边的平方=-=7或+=25.查看答案和解析>>
科目:初中数学 来源:广东省2017届九年级上学期第二次月考数学试卷 题型:解答题
在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长15米)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成,若设花园平行于墙的一边长为x(m),花园的面积为y(m2).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)满足条件的花园面积能达到200m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,花园的面积最大,最大面积是多少?
(1)y=﹣x2+20x(0<x≤15);(2)花园面积不能达到200m2;(3)当x=15时,花园的面积最大,最大面积为187.5m2. 【解析】试题分析:(1)设花园靠墙的一边长为x(m),另一边长为,用面积公式表示矩形面积; (2)就是已知y=200,解一元二次方程,但要注意检验结果是否符合题意;即结果应该是0<x≤15. (3)由于0<x≤15,对称轴x=20,即顶点不在...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:单选题
在半径为2的圆中,弦AB的长为2,则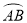 的长等于( )
的长等于( )
A. 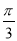 B.
B.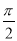 C.
C.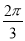 D.
D.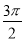
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com