
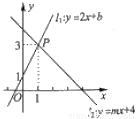
如图所示,直线l1:y=2x+b与直线l2:y=mx+4相交于点P(1,3),利用图像:
(1)解关于x,y的二元一次方程组: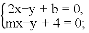
(2)解关于x的一元一次不等式:2x+b>mx+4.
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2017年甘肃省中考数学模拟试卷 题型:填空题
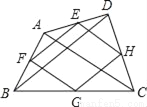
如图,连接四边形ABCD各边中点,得到四边形EFGH,还要添加_____条件,才能保证四边形EFGH是矩形.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年上学期苏州市初三数学期末综合检测 题型:单选题
下列方程中,是关于
A. 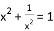 B.
B. 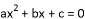 C.
C. 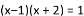
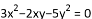
查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期中数学试卷 题型:单选题
关于x的分式方程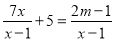 有增根,则m的值为( )
有增根,则m的值为( )
A. 1 B. 3 C. 4 D. 5
C 【解析】试题解析:方程两边都乘(x﹣1), 得7x+5(x﹣1)=2m﹣1, ∵原方程有增根, ∴最简公分母(x﹣1)=0, 解得x=1, 当x=1时,7=2m﹣1, 解得m=4, 所以m的值为4. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省聊城市莘县2017-2018学年八年级(上)期中数学试卷 题型:单选题
下列说法正确的是( )
A. 角是轴对称图形,它的平分线就是它的对称轴
B. 等腰三角形的内角平分线,中线和高三线合一
C. 直角三角形不是轴对称图形
D. 等边三角形有三条对称轴
D 【解析】试题解析:A、角是轴对称图形,它的平分线所在直线是它的对称轴,故错误,不符合题意; B、等腰三角形的底边的中线、角平分线及高三线合一,故错误,不符合题意; C、直角三角形不一定是轴对称图形,故错误,不符合题意; D、等边三角形有三条对称轴,正确,符合题意; 故选D.查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
已知直线l与直线y=-2x平行,且经过点(-1,-2)求直线l与坐标轴围成的三角形的面积.
该函数图像与坐标轴围成的三角形的面积为4. 【解析】试题分析:根据直线l与直线y=-2x平行,可设直线l的解析式为y=-2x+b,根据直线l经过点(-1,-2),即可求得b值,再求得直线l与坐标轴的交点坐标,即可求得围成的三角形的面积. 试题解析: 设一次函数关系式为y=-2x+b, 将(-1,-2)代入上式得-2×(-1)+b=-2,解得b=-4, 即y=-2x-4...查看答案和解析>>
科目:初中数学 来源:安徽省亳州市利辛县2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A. 点(0,k)在l上
B. l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大
D. l经过第一、二、三象限
D 【解析】A.当x=0时,y=k,即点(0,k)在l上,故此选项正确; B.当x=﹣1时,y=﹣k+k=0,此选项正确; C.当k>0时,y随x的增大而增大,此选项正确; D.不能确定l经过第一、二、三象限,此选项错误; 故选D.查看答案和解析>>
科目:初中数学 来源:内蒙古鄂尔多斯市2017-2018学年第一学期期中试卷初一数学. 题型:填空题
在数轴上与表示1的点的距离为3个单位长度的点所表示的数是________.
-2和4 【解析】设该点表示的数为x,则|1?x|=3,解得x=?2或4. 故答案为:?2或4.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷 题型:解答题
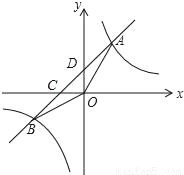
如图,点A(m,4),B(﹣4,n)在反比例函数y=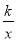 (k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(k>0)的图象上,经过点A、B的直线与x轴相交于点C,与y轴相交于点D.
(1)若m=2,求n的值;
(2)求m+n的值;
(3)连接OA、OB,若tan∠AOD+tan∠BOC=1,求直线AB的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com