
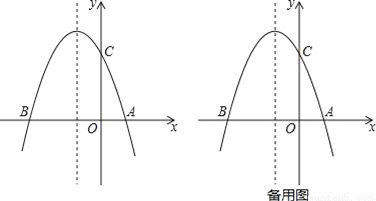
如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.
(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:安徽省霍邱县2017-2018学年度第一学期期中考试八年级数学试卷(答案版) 题型:单选题
函数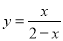 中自变量
中自变量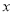 的取值范围是( )
的取值范围是( )
A. 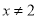 B.
B. 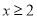 C.
C. 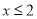 D.
D. 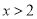
查看答案和解析>>
科目:初中数学 来源:黄金30题系列七年级数学 大题易丢分 题型:解答题
若a与2互为相反数,c与d互为倒数,m的平方与它本身相等,请你求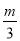 -
-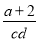 +2cd的值.
+2cd的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:填空题
点A(﹣2,a)和点B(b,﹣5)关于x轴对称,则a+b=_____.
3 【解析】由题意得, b=-2,a=5,所以a+b=3.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:单选题
一个等腰三角形的两个内角和为100°,则它的顶角度数为( )
A. 50° B. 80° C. 50°或80° D. 20°或80°
D 【解析】设顶角时x,则x+y=100°,2x+y=180°,解得x=80°,y=20°;x+y=100°, x+2y=180°,解得x=20°,y=80°.所以选D.查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:解答题
已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+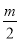 -
-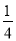 =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么平行四边形ABCD的周长是多少?
(1)m=1时,四边形ABCD是菱形,菱形ABCD的边长是;(2)平行四边形ABCD的周长是5. 【解析】试题分析: (1)∵四边形ABCD是菱形, ∴AB=AD, ∴△=0,即m2﹣4(﹣)=0, 整理得:(m﹣1)2=0, 解得m=1, 当m=1时,原方程为x2﹣x+=0, 解得:x1=x2=0.5, 故当m=1时,四边形ABCD是菱形,菱形的边...查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:填空题
k_____时,关于x的方程kx2﹣3x=2x2+1是一元二次方程.
≠2 【解析】原方程可化为: (k﹣2)x2﹣3x﹣1=0 ∵方程是一元二次方程, ∴k﹣2≠0 故答案是:≠2.查看答案和解析>>
科目:初中数学 来源:四川江油小溪坝中学2017年秋七年级数学第三学月检测题 题型:解答题
解方程:(1)x-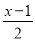 =2-
=2-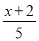 ;(2)
;(2)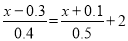
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级12月月考数学试卷 题型:单选题
如图,点B在线段AC上,且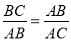 ,设AC=1,则BC的长是( )
,设AC=1,则BC的长是( )

A. 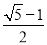 B.
B. 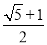 C.
C. 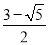 D.
D. 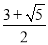
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com