
一元二次方程x2+4=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
C 【解析】a=1,b=0,c=4, ∵△=﹣16<0, ∴方程无实数根, 故选C. 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:浙江省杭州市2018届九年级上学期期中数学试卷 题型:单选题
从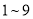 这九个自然数中任取一个,是
这九个自然数中任取一个,是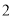 的倍数的概率是( ).
的倍数的概率是( ).
A. 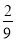 B.
B. 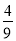 C.
C. 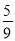 D.
D. 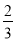
查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第6章 反比例函数 单元测试卷 题型:单选题
已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A. 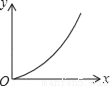 B.
B.  C.
C. 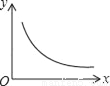 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:填空题
意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
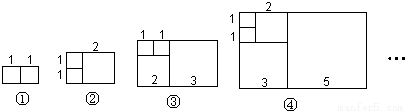
查看答案和解析>>
科目:初中数学 来源:2017-2018学年广东省汕头市潮南区九年级(上)期末数学试卷(a卷) 题型:单选题
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在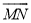 上,且不与M,N重合,当P点在
上,且不与M,N重合,当P点在 上移动时,矩形PAOB的形状、大小随之变化,则AB的长度( )
上移动时,矩形PAOB的形状、大小随之变化,则AB的长度( )
A. 变大 B. 变小 C. 不变 D. 不能确定
C 【解析】试题解析:∵PAOB是扇形OMN的内接矩形, ∴AB=OP=半径, 当P点在上移动时,半径一定,所以AB长度不变, 故选C.查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017-2018学年度上期教学质量监测八年级数学试卷 题型:解答题
随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
(1)每台B型空气净化器、每台A型空气净化器的进价分别为1200元,1500元; (2)应将B型空气净化器的售价定为1600元. 【解析】试题分析:(1)设每台B种空气净化器为x元,A种净化器为(x+300)元,根据用6000元购进B种空气净化器的数量与用7500元购进A种空气净化器的数量相同,列方程求解; (2)根据总利润=单件利润×销量列出一元二次方程求解即可. 试题解...查看答案和解析>>
科目:初中数学 来源:广西北海市银海区2017-2018学年度上期教学质量监测八年级数学试卷 题型:填空题
如图,在平面直角坐标系中,点A(8,0),点P(0,m),将线段PA绕着点P逆时针旋转90°,得到线段PB,连接AB,OB,则BO+BA的最小值为_______________ .
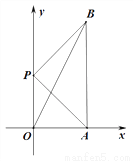
查看答案和解析>>
科目:初中数学 来源:江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
某制衣厂计划若干天完成一批服装的订货任务.如果每天生产服装33套,那么就比订货任务少生产150套;如果每天生产服装42套,那么就比原计划提前2天完成任务.这批服装的订货任务是多少套?原计划多少天完成任务?
这批服装的订货任务是1008套,原计划26天完成任务. 【解析】设原计划x天完成任务,根据订货任务是一定的这一等量关系建立方程即可求解. 【解析】 设原计划x天完成任务,由题意得: , 解得: , 所以. 答:这批服装的订货任务是1008套,原计划26天完成任务.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第七章达标检测卷 题型:单选题
已知点P(2a﹣5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是( )
A. 1 B. ﹣1 C. 0 D. 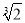
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com