练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简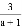：（﹣a+1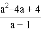）÷，并从0，﹣1，2中选一个合适的数作为a的值代入求值．

    1. 【解析】试题分析：首先把括号的分式通分化简，后面的分式的分子分解因式，然后约分化简，接着计算分式的乘法，最后代入数值计算即可求解． 试题解析：原式===； 当a=0时，原式=1．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型：解答题

    已知|a|=8，|b|=6且a+b＜0，求2a﹣b的值．

    ﹣22或﹣10. 【解析】试题分析：先由绝对值的性质求得a、b的值，然后根据a+b＜0，确定出a、b的取值情况，然后代入数值进行计算即可． 试题解析：∵|a|=8，|b|=6， ∴a=±8，b=±6， ∵a+b＜0， ∴a=﹣8，b=6，或a=﹣8，b=﹣6， 当a=﹣8，b=6时，2a﹣b=2×（﹣8）﹣6=﹣16﹣6=﹣22； 当a=﹣8，b=﹣6时，...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖南省郴州市中考数学模拟试卷 题型：单选题

    如图，是我们学过的用直尺和三角尺画平行线的方法示意图，画图的原理是（　　）

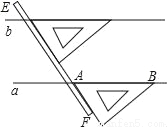
    A. 同位角相等，两直线平行 B. 内错角相等，两直线平行

    C. 两直线平行，同位角相等 D. 两直线平行，内错角相等

    A 【解析】三角板的∠CAB，沿着FE进行平移后角的大小没变，而平移前后的两个角是同位角，所以画图原理是“同位角相等，两直线平行”．

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：单选题

    已知等腰△ABC的三个顶点都在半径为5的⊙O上，如果底边BC的长为8，那么BC边上的高为（　　）

    A. 2 B. 5 C. 2或8 D. 4

    C 【解析】【解析】 分为两种情况：①如图1，当圆心在三角形的内部时，连接AO并延长交BC于D点，连接OB，∵AB=AC，∴弧AB=弧AC，根据垂径定理得AD⊥BC，则BD=4，在Rt△ODB中，由勾股定理得：OB2=OD2+BD2，∵OB=5，BD=4，∴OD=3，∴高AD=5+3=8； ②当圆心在三角形的外部时，如图2， 三角形底边BC上的高AD=5﹣3=2． 所以B...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：单选题

    25的算术平方根是（ ）

    A．5 B．-5 C．±5 D．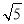

    A． 【解析】 试题解析：∵（5）2=25， ∴25的算术平方根是5． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

    如图，点F、C在线段BE上，且∠1=∠2，BC=EF，若要使△ABC≌△DEF，则还需补充一个条件________，依据是________．

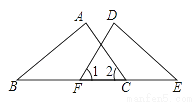
    AC=DF SAS 【解析】AC=DF， 在△ABC和△DEF中， ，∴△ABC≌△DEF（SAS）， 故答案为：AC=DF，SAS．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年八年级上期末模拟数学试卷 题型：单选题

    下列命题其中真命题的个数是（  ）

    （1）长度相等的弧是等弧；

    （2）圆是轴对称图形，它的对称轴是过圆心的弦

    （3）相等的圆心角所所对的弦相等；

    （4）在同圆或者等圆中，相等的两弦所对的弧相等．

    A. 0 B. 1 C. 2 D. 3

    A 【解析】（1）在同圆或等圆中长度相等的弧是等弧，故（1）错误；（2）圆是轴对称图形，它的对称轴是过圆心的直线，故（2）错误；（3）在同圆或等圆中相等的圆心角所对的弦相等，故（3）错误；（4）在同圆或者等圆中，相等的两弦所对的优弧相等，劣弧相等，故（4）错误；所以真命题的个数是0， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型：解答题

    解方程：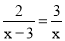

    所以是原方程的解． 【解析】试题分析：分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解． 试题解析：方程两边同乘以，得 ． ． 检验：把代入，得， 所以是原方程的解．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

    如图：已知AB是⊙O的直径，BC是⊙O的切线，OC与⊙O相交于点D，连结AD并延长，与BC相交于点E。

    （1）若BC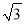＝，CD＝1，求⊙O的半径；

    （2）取BE的中点F，连结DF，求证：DF是⊙O的切线。

    （1）【解析】 ∵AB是⊙O的直径，BC是⊙O的切线∴AB⊥BC， 设⊙O的半径为，在Rt△OBC中，∵ ∴，解得＝1，∴⊙O的半径为1 （2）连结OF，∵OA＝OB，BF＝EF，∴OF∥AE，∠A＝∠2 又∵∠BOD＝2∠A，∴∠1＝∠2， 又∵OB＝OD、OF＝OF∴△OBF≌△ODF， ∴∠ODF＝∠OBF＝900，即OD⊥DF，∴FD是⊙O的切线。 ...

    查看答案和解析>>

    同步练习册答案