
p在数轴上的位置如图所示, 化简|p+1|-|p-2|=_________.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:山东省淄博市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
若a,b,c为三角形的三边,则下列各组数据中,不能组成直角三角形的是( )
A. a=8,b=15,c=17 B. a=3,b=5,c=4
C. a=4,b=8,c=9 D. a=9,b=40,c=41
C 【解析】选项A, ,根据勾股定理的逆定理可得以a、b、c为三边的三角形是直角三角形;选项B, ,根据勾股定理的逆定理可得以a、b、c为三边的三角形是直角三角形;选项C, ,根据勾股定理的逆定理可得以a、b、c为三边的三角形不是直角三角形;选项D, ,根据勾股定理的逆定理可得以a、b、c为三边的三角形是直角三角形.故选C.查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
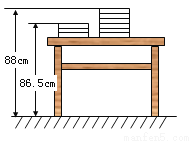
新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:
(1)每本书的高度为 cm,课桌的高度为 cm;
(2)当课本数为x(本)时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离 (用含x的代数式表示);
(3)桌面上有55本与题(1)中相同的数学课本,整齐叠放成一摞,若有18名同学各从中取走1本,求余下的数学课本高出地面的距离.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
计算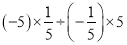 结果正确的是( )
结果正确的是( )
A. 25 B. -25 C. -1 D. 1
A 【解析】【解析】 =1×5×5=25.故选A.查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型:解答题
如图,在平整地面上,若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
(1)这个几何体由______个小正方体组成.
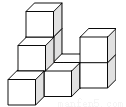
(2)在下面网格中画出左视图和俯视图.
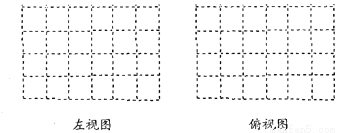
(3)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
(1)10;(2)作图见解析;(3)3200cm2. 【解析】试题分析:(1)从左往右三列小正方体的个数依次为:6,2,2,相加即可; (2)由已知条件可知,左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1.据此可画出图形; (3)根据露出的小正方体的面数,可得几何体的表面积. 试题解析:【解析】 (1)这个几何体由6+2+...查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型:填空题
对于有理数a、b,定义一种新运算a☆ b=a2﹣|b|,则2☆(﹣3)=______
1 【解析】【解析】 2☆(﹣3)=22﹣|﹣3|=4﹣3=1.故答案为:1.查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016-2017下学期初一期末数学试卷 题型:单选题
如图,一副三角尺按不同的位置摆放,摆放位置中∠α=∠β的图形有( )

A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】【解析】 根据角的和差关系可得第一个图形∠α=∠β=45°,根据同角的余角相等可得第二个图形∠α=∠β,根据等角的补角相等可得第三个图形∠α=∠β,第四个图形∠α+∠β=180°,不相等,因此∠α=∠β的图形个数共有3个.故选C.查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市校2017-2018学年七年级上册期末教学质量检测数学试卷 题型:填空题
矩形的周长为30,若一边长用字母x表示,则此矩形的面积是__.
x(15﹣x) 【解析】∵周长是30,∴相邻两边的和是15, ∵一边是x,∴另一边是15?x. ∴面积是:x(15?x). 故答案为:x(15?x).查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
如图,已知抛物线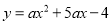 交
交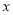 轴于点
轴于点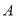 、点
、点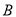 ,交
,交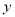 轴于点C,且S△ABC=6.
轴于点C,且S△ABC=6.
(1)求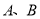 两点的坐标;
两点的坐标;
(2)求△ABC的外接圆与抛物线的对称轴的交点坐标;
(3)点E为抛物线上的一动点(点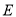 异于
异于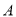 ,且
,且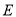 在对称轴右侧),直线
在对称轴右侧),直线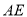 交对称轴于N,
交对称轴于N,
直线BE交对称轴于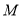 ,对称轴交
,对称轴交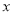 轴于
轴于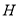 ,试确定
,试确定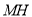 、
、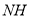 的数量关系并说明理由.
的数量关系并说明理由.
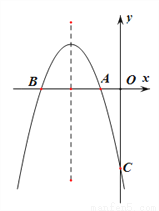
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com