
已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=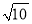 .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.
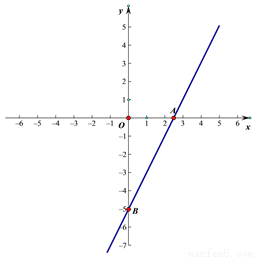

图1 图2
(1)C(1,-3),D(0,-6);(2)P(0, ) 、P(0, ) 、P(0,0)、P(0, );(3)N(5,5)或N()或N(). 【解析】试题分析:(1)先确定点C的坐标,设点D坐标为(0,d)(d<0),则有CD2=(1-0)2+(-3-d)2=,解之即可得; (2)分别以点C、点D为圆心,CD为半径画圆,圆与y轴即为满足条件的点,作CD的中垂线与y轴的交点也满足条件,然...科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:解答题
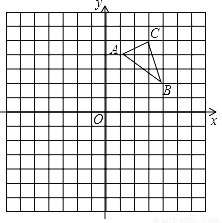
如图所示,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度)
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于原点对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出线段OB旋转到OB2扫过图形的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型:单选题
已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是( )
A. 相切 B. 相离 C. 相离或相切 D. 相切或相交
D 【解析】试题分析:当OP垂直于直线l时,即圆心O到直线l的距离d=2=r,⊙O与l相切;当OP不垂直于直线l时,即圆心O到直线l的距离d<2=r,⊙O与直线l相交.所以直线l与⊙O的位置关系是相切或相交.故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
比较大小: 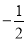 _____
_____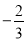 .(填“>”或“<”号).
.(填“>”或“<”号).
查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:单选题
已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )
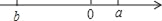
A. 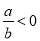 B. a﹣b>0 C. a+b>0 D. ab<0
B. a﹣b>0 C. a+b>0 D. ab<0
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
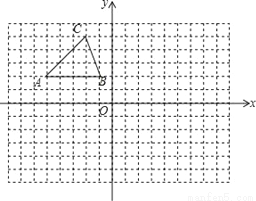
在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为______;
(4)试在y轴上找一点Q,使得点Q到B2、C2两点的距离之和最小,此时,QB2+QC2的最小值为______.
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
如图,Rt△ABC中,∠ACB=90°,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②∠DCP=45°;③BP垂直平分CE;④GF+ FC =GA;其中正确的判断有______________.(填序号)

查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
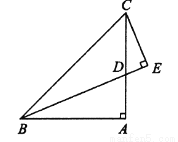
如图,在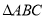 中,
中, 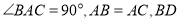 平分
平分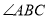 ,
, 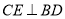 于点
于点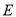 .
.
(1)求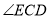 的度数.
的度数.
(2)求证: 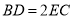 .
.
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
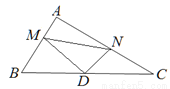
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
A. 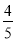 B.
B. 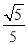 C.
C. 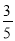 D.
D. 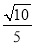
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com