练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

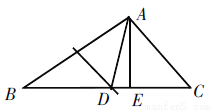
    如图，△ABC中，BC=8，AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长等于______.

    4cm 【解析】因为AB的中垂线交BC于D，AC的中垂线交BC与E，所以AD=DB，AE=CE. △ADE的周长为AD+DE+AE=BD+DE+EC=BC=8. 故答案为8.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章第一节《一元二次方程》提高练习 题型：解答题

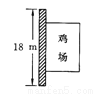
    如图所示，有一个面积为120m2的长方形鸡场，鸡场一边靠墙（墙长18m），另三边用竹篱笆围成，若所围篱笆的总长为32m，求鸡场的长和宽各为多少米. （只列方程）

    x2－32x＋240＝0 【解析】试题分析：设平行于墙的边长为m，则垂直于墙的边长为m，根据长方形的面积公式，列出方程. 试题解析： 设平行于墙的边长为m，则垂直于墙的边长为m，由题意得x·＝120， 即

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型：解答题

    如图所示，在△ABC中，∠ABC=∠ACB．

    （1）尺规作图：过顶点A，作△ABC的角平分线AD；(不写作法，保留作图痕迹)

    （2）在AD上任取一点E，连接BE、CE．求证：BE=CE．

    （1）作图见解析；（2）证明见解析. 【解析】试题分析：（1）以A为圆心，以任意长为比较画弧，分别交AB和AC于一点，分别以这两点为圆心，以大于这两点之间的距离为半径画弧，两弧交于一点，过这点和A作射线，交BC于D，则，AD为所求； （2）推出∠BAE=∠CAE，根据SAS证△BAE和△CAE全等即可． 试题解析：（1）【解析】 如图所示： （2）证明：∵AD是△ABC的...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型：单选题

    一个三角形的两边长分别是3和7，则第三边长可能是( )

    A. 2 B. 3 C. 9 D. 10

    C 【解析】设第三边长为x，由题意得： 7-3

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：解答题

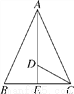
    如图，在△ABC中，已知AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝125°，求∠ACB和∠BAC的度数．

    ∠ACB＝70°；∠BAC＝40°. 【解析】试题分析:根据等腰三角形三线合一的性质可得AE⊥BC，再求出∠CDE，然后根据直角三角形两锐角互余求出∠DCE，根据角平分线的定义求出∠ACB，再根据等腰三角形两底角相等列式进行计算即可求出∠BAC． 试题解析：∵AB=AC，AE平分∠BAC， ∴AE⊥BC（等腰三角形三线合一）， ∵∠ADC=125°， ∴∠CDE=55...

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：单选题

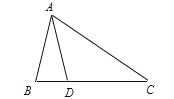
    如图，在△ABC中，D为BC上一点，且AB＝AD＝DC，∠B＝80º，则∠C等于 （ ）

    A．20º B．30º C．40º D．50º

    C 【解析】 试题分析：根据AB=AD可得：∠ADB=∠B=80°，根据外角的性质可得：∠ADB=∠DAC+∠C，根据AD=CD可得：∠DAC=∠C，则∠C=40°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：单选题

    如图，C、D是线段AB上两点，分别以点A和点B为圆心，AD、BC长为半径作弧，两弧相交于点M，连接AM、BM，测量∠AMB的度数，结果为（　　）

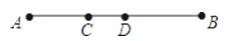
    A. 100° B. 110° C. 120° D. 130°

    B 【解析】根据题意作出图形，然后利用量角器测量即可， 如图，∠AMB=110°， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第19章 一次函数 单元检测卷 题型：填空题

    如图，已知一次函数y=kx+b，观察图象回答下列问题：x________ 时，kx+b＜0．

    ＜2.5 【解析】【解析】 由图象可知：当x＜2.5时，kx+b＜0．故答案为：＜2.5．

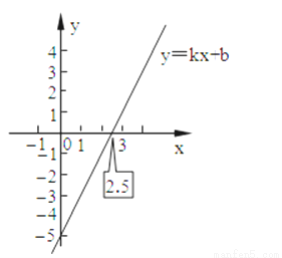
    查看答案和解析>>

    科目：初中数学 来源：人教版初中数学九年级上册第二十二章《实际问题与二次函数》同步测试 题型：解答题

    如图，有一座抛物线型拱桥，已知桥下在正常水位AB时，水面宽8m，水位上升3m， 就达到警戒水位CD，这时水面宽4m，若洪水到来时，水位以每小时0.2m的速度上升，求水过警戒水位后几小时淹到桥拱顶．

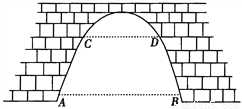
    5小时． 【解析】试题分析； 首先在图中建立合适的坐标系（这里选择AB所在直线为x轴，AB的垂直平分线为y轴，也可另外建立），然后根据题目中的已知条件可得A、B、C、D四点的坐标，设出解析式，代入相应点的坐标建立方程（组），解方程（组）求得待定系数的值得到解析式，由解析式可得顶点E的坐标，再结合题中条件可解得答案； 试题解析： 如上图，以AB所在直线为x轴，AB的垂直平分线...

    查看答案和解析>>

    同步练习册答案