
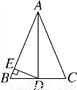
��ͼ���ڡ�ABC�У�AB��AC��13��BC��10����DΪBC���е㣬DE��AB������Ϊ��E����DE�ij�Ϊ(����)
A. 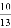 B.
B. 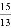 C.
C. 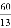 D.
D. 
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ��������תһ���γ�һ�������壬�������Ƶ������� �� ����
���� B������ C������ D��ˮͰ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�人����ɽ��2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
һ����λ����λ�ϵ�������1��ʮλ�ϵ�������x����1��x��λ�öԵ��õ�һ������λ����������λ����ԭ��λ��С18������з���_____��
10x+1=10+x+18 ����������������������⣬�ɵ�ԭ��Ϊ10x+1������Ϊ10+x�� �������⣬��10x+1=10+x+18�� �ʴ�Ϊ��10x+1=10+x+18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ2017-2018ѧ����꼶��ѧ�ڵڶ���ѧ������ѧ�Ծ� ���ͣ������
��ͼ����ABD=��ACD=90�㣬��1=��2.
��֤��ADƽ�֡�BDC��
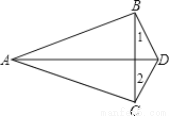
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ2017-2018ѧ����꼶��ѧ�ڵڶ���ѧ������ѧ�Ծ� ���ͣ������
���⡰ͬλ����ȣ���ֱ��ƽ�С����������ǣ� ��
��ֱ��ƽ�У�ͬλ����ȣ� �������������������һ�����������ͽ��ۻ����͵õ����������⣮ �������� ���⣺��ͬλ����ȣ���ֱ��ƽ�У����������ǡ�ͬλ����ȡ��������ǡ���ֱ��ƽ�С��� ���������������ǡ���ֱ��ƽ�У�ͬλ����ȣ��� �ʴ�Ϊ������ֱ��ƽ�У�ͬλ����ȡ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ2017-2018ѧ����꼶��ѧ�ڵڶ���ѧ������ѧ�Ծ� ���ͣ���ѡ��
����ʽ��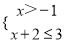 �Ľ⼯�������ϱ�ʾΪ�� ����
�Ľ⼯�������ϱ�ʾΪ�� ����
A. 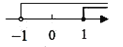
B. 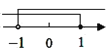
C. 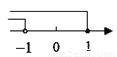
D. 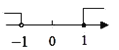
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ͨ��2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
��ͼ���ۿ�A�ڹ۲�վO����������OA=4km��ij���Ӹۿ�A�������ر�ƫ��15�㷽����һ�ξ����B������ʱ�ӹ۲�վO����øô�λ�ڱ�ƫ��60��ķ�����ô����еľ��루��AB�ij�����
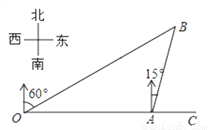
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��ͨ��2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��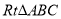 ��
�У� 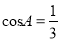 ����ô
����ô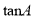 ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A. 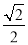 B.
B. 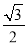 C.
C. 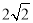 D.
D. 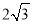
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ�����꼶12���¿���ѧ�Ծ� ���ͣ������
����
��1����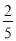 +����
+����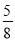 ��
��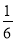 +
+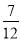 ����24
����24
��2����12010����1��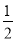 ��3����|3������3��2|
��3����|3������3��2|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com