练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列各式中，能用完全平方公式分解因式的是(　　)

    A. 16x2＋1 B. x2＋2x－1

    C. a2＋2ab＋4b2 D. x2－x＋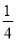

    D 【解析】解：A． 16x2＋1只有两项，不能用完全平方公式分解； B． x2＋2x-1，不能用完全平方公式分解； C． a2＋2ab＋4b2，不能用完全平方公式分解； D． x2－x＋=，能用完全平方公式分解． 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    把抛物线y=(x+2)2向下平移2各单位长度，再向右平移2个单位长度，所得抛物线的解析式为 （ ）

    A. y=( 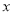+2)2+2 B. y=2(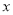-1)2+4

    C. y= 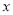2+2 D. y= 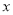2-2

    D 【解析】∵二次函数y=(x+2)2的顶点坐标为(?2,0) ∴图象向下平移2个单位长度,再向右平移2个单位长度后,顶点坐标为(0,?2)， 由顶点式得,平移后抛物线解析式为：y=x2?2， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型：单选题

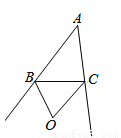
    如图，点O是△ABC的两外角平分线的交点，下列结论：①OB=OC；②点O到直线

    AB、AC的距离相等；③点O到△ABC的三边所在直线的距离相等；④点O在∠A的

    平分线上，正确的个数有( )

    A. 1个 B. 2个 C. 3个 D. 4个

    C 【解析】试题解析：如图，过点O作OE⊥AB于E，作OF⊥BC于F，作OG⊥AC于G， ∵点O是△ABC的两外角平分线的交点， ∴OE=OG，OF=OG， ∴OE=OF=OG， ∴点O在∠B的平分线上，故②③④正确， 只有点G是AC的中点时，BO=CO，故①错误， 综上所述，说法正确的是②③④. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型：填空题

    已知m2＋n2－6m＋10n＋34＝0，则m＋n＝ __________

    -2 【解析】【解析】 ∵(m-3)2＋(n+5)2=0，∴m-3=0，n+5=0，解得：m=3，n=-5，∴m+n=3-5=-2．故答案为：-2．

    查看答案和解析>>

    科目：初中数学 来源：湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型：单选题

    计算(0.5×105)3×(4×103)2的结果是

    A. 2×1013 B. 0.5×1014 C. 2×1021 D. 8×1021

    C 【解析】根据同底数幂的乘法的性质，幂的乘方的性质，积的乘方的性质进行计算． 【解析】 （0.5×105）3×（4×103）2=0.125×1015×16×106=2×1021． 故选C． 本题考查同底数幂的乘法，幂的乘方，积的乘方，理清指数的变化是解题的关键．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型：解答题

    在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ．

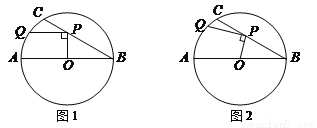
    （1）如图1，当PQ∥AB时，求PQ的长度；

    （2）如图2，当点P在BC上移动时，求PQ长的最大值．

    （1）；（2）． 【解析】试题分析：（1）在Rt△OPB中，由OP=OB·tan∠ABC可求得OP=，连接OQ，在Rt△OPQ中，根据勾股定理可得PQ的长；（2）由勾股定理可知OQ为定值，所以当当OP最小时，PQ最大．根据垂线段最短可知，当OP⊥BC时OP最小，所以在Rt△OPB中，由OP=OB·sin∠ABC求得OP的长；在Rt△OPQ中，根据勾股定理求得PQ的长． 试题解析：【解析...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型：解答题

    一个不透明的口袋中装有2个红球（记为红球1、红球2），1个白球、1个黑球，这些球除颜色外都相同，将球搅匀．

    （1）从中任意摸出1个球，恰好摸到红球的概率是　　　

    （2）先从中任意摸出一个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表），求两次都摸到红球的概率．

    （1）；（2）P（两次摸到红球）=． 【解析】试题分析：（1）根据4个小球中红球的个数，即可确定出从中任意摸出1个球，恰好摸到红球的概率； （2）列表得出所有等可能的情况数，找出两次都摸到红球的情况数，即可求出所求的概率． 试题解析：（1）4个小球中有2个红球， 则任意摸出1个球，恰好摸到红球的概率是； （2）列表如下： 红 红 ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型：单选题

    在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是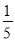，则n的值为（ ）

    A. 3 B. 5 C. 8 D. 10

    C 【解析】试题分析：在一个不透明的盒子里有2个红球和n个白球，这些球除颜色外其余完全相同，摇匀后随机摸出一个，摸到红球的概率是，而其概率为，因此可得=，解得n=8. 故选：B．

    查看答案和解析>>

    科目：初中数学 来源：2017年河南省中考数学三模试卷 题型：单选题

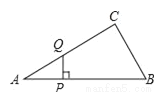
    如图，△ABC中，∠ACB=90°，∠A=30°，AB=16，点P是斜边AB上任意一点，过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致是（　　）

    A. B. C. D.

    D 【解析】【解析】 当点Q在AC上时，∵∠A=30°，AP=x，∴PQ=xtan30°=，∴y=×AP×PQ=×x×=x2； 当点Q在BC上时，如下图所示： ∵AP=x，AB=16，∠A=30°，∴BP=16﹣x，∠B=60°，∴PQ=BP•tan60°=（16﹣x），∴ =AP•PQ= = ，∴该函数图象前半部分是抛物线开口向上，后半部分也为抛物线开口向下．故选D．

    查看答案和解析>>

    同步练习册答案