练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    两个点关于原点对称时，它们的坐标符号相反，即点P(x，y)关于原点的对称点为P′____.

    (-x，-y). 【解析】试题分析：两点关于原点对称，则对称的两个点的横纵坐标分别互为相反数．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型：解答题

    已知△ABC的三个顶点的坐标分别是A（﹣2，4），点B（0，1），点C（2，2）．

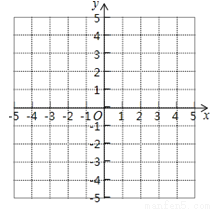
    （1）在所给的平面直角坐标系中画出△ABC，并将△ABC向左平移一个单位，向下平移两个单位得到△A’B’C’，画出△A’B’C’．

    （2）直接写出点A到x轴，y轴的距离分别是多少？

    （3）求出△ABC的面积．

    （1）作图见解析； （2）4，2； （3）4． 【解析】试题分析：（1）平移点，按照要求作图. (2)横坐标绝对值是到y轴距离，纵坐标绝对值是到x轴距离. (3)利用矩形面积减去3个直角三角形面积. 试题解析：(1) （2）A（﹣2，4）,，到x轴距离4, 到y轴距离2. （3）．

    查看答案和解析>>

    科目：初中数学 来源：初一数学第一学期6.1数据的收集 同步练习 题型：单选题

    某校对全体学生开展心理健康知识测试，七、八、九三个年级共有800名学生，各年级的合格人数如表所示，则下列说法正确的是（　　）

    年级

    七年级

    八年级

    九年级

    合格人数

    270

    262

    254

    A. 七年级的合格率最高

    B. 八年级的学生人数为262名

    C. 八年级的合格率高于全校的合格率

    D. 九年级的合格人数最少

    D 【解析】因为合格率=合格人数÷年级总人数，而题中不知道各个年级的具体人数，因此无法比较合格率的高低，故A、C错误；八年级的合格人数为262人，故B错误；270>262>254，故九年级的合格人数最少，故D正确， 故选D.

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型：单选题

    如图，将△ABC绕点C(0，1)旋转180°得到△A′B′C，设点A的坐标为(a，b)，则点A′的坐标为( )

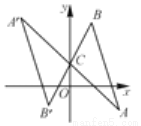
    A. (-a，-b) B. (-a，-b-1) C. (-a，-b+1) D. (-a，-b+2)

    D 【解析】试题分析：根据题意，点A、A′关于点C对称，设点A′的坐标是（x，y），则=0， =1，解得x=-a，y=-b+2，∴点A′的坐标是(-a，-b+2)．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型：单选题

    将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )

    A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)

    D 【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：解答题

    已知抛物线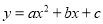的对称轴为x=2，且经过点（1,4）和（5,0），试求该抛物线的表达式。

    【解析】试题分析：根据题意，对称轴为直线x=2，图象经过点（5，0），根据抛物线的对称性，可知图象经过另一点（-1，0），设抛物线的交点式y=a（x+1）（x-5），把点（1，4）代入即可．本题也可以由对称轴为直线x=-=2，再将两点坐标代入，求解三元一次方程组. 解：根据抛物线对称轴为直线x=2，且抛物线过点（5,0）， 可知抛物线与x轴另一交点为（-1,0）， 则设抛物线解析...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质（1）测试 题型：填空题

    若二次函数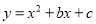的图象经过点（-1,0），（1，-2），当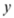随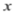的增大而增大时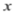，的取值范围是____________。

    x> 【解析】将（-1,0），（1，-2）代入函数解析式得解得 则函数解析式为y=x2-x-2=（x-）2-， 根据抛物线性质可知当x>时，函数值y随x的增大而增大. 故答案为x>.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型：解答题

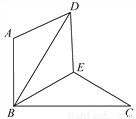
    如图，△BAD是由△BEC在平面内绕点B旋转60°而得，且AB⊥BC，BE＝CE，连接DE.

    （1）求证：△BDE≌△BCE；

    （2）试判断四边形ABED的形状，并说明理由．

    证明见解析. 【解析】试题分析：（1）根据旋转的性质可得DB=CB，∠ABD=∠EBC，∠ABE=60°，然后根据垂直可得出∠DBE=∠CBE=30°，继而可根据SAS证明△BDE≌△BCE； （2）根据（1）以及旋转的性质可得，△BDE≌△BCE≌△BDA，继而得出四条棱相等，证得四边形ABED为菱形． （1）证明：∵△BAD是由△BEC在平面内绕点B旋转60°而得， ∴...

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级上册数学 23.1图形的旋转（1）测试 题型：解答题

    某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

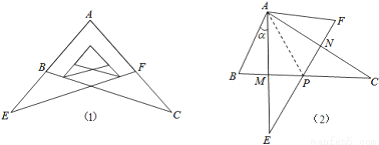
    （1）求证：AM=AN；

    （2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

    （1）证明见解析；（2）当旋转角α=30°时，四边形ABPF是菱形．理由见解析. 【解析】 试题分析：（1）根据旋转的性质得出AB=AF，∠BAM=∠FAN，进而得出△ABM≌△AFN得出答案即可； （2）利用旋转的性质得出∠FAB=120°，∠FPC=∠B=60°，即可得出四边形ABPF是平行四边形，再利用菱形的判定得出答案． 试题解析：（1）∵用两块完全相同的且含60°...

    查看答案和解析>>

    同步练习册答案