
如果一个三角形的两边长分别为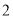 和
和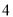 ,则第三边长可能是( ).
,则第三边长可能是( ).
A. 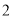 B.
B. 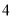 C.
C. 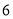 D.
D. 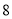
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
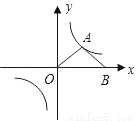
如图,点A为反比例函数y=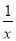 的图象上一点,B点在x轴上且OA=BA,则△AOB的面积为_____.
的图象上一点,B点在x轴上且OA=BA,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源:上海市普陀区(五四制)2017-2018学年六年级上学期期末考试数学试卷 题型:填空题
分解素因数:24 =________________ .
【解析】从每个数最小的质因数开始去除,除到商是质数为止,最后把这个合数写成除数和商相乘的形式,故24=2×2×2×3, 故答案为:2×2×2×3.查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:填空题
因式分【解析】
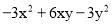 =
=
查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:单选题
下列多边形中,内角和是外角和的两倍的是( )
A. 四边形 B. 五边形 C. 六边形 D. 八边形
C 【解析】【解析】 设多边形边数为n,由题意得:(n﹣2)•180°=2×360°,解得n=6,所以这个多边形是六边形.故选C.查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:解答题
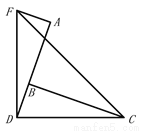
如图,已知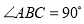 ,
,  是直线
是直线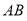 上的点,
上的点, 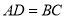 ,过点
,过点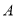 作
作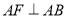 ,并截取
,并截取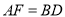 ,连接
,连接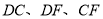 ,判断△
,判断△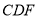 的形状并证明.
的形状并证明.
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:单选题
小明用尺规作图作△ABC边AC上的高BH,作法如下:
①分别以点D,E为圆心,大于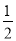 DE的长为半径作弧,两弧交于F;
DE的长为半径作弧,两弧交于F;
②作射线BF,交边AC于点H;
③以B为圆心,BK长为半径作弧,交直线AC于点D和E;
④取一点K,使K和B在AC的两侧;
所以,BH就是所求作的高. 其中顺序正确的作图步骤是( )
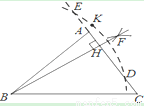
A. ①②③④ B. ④③②① C. ②④③① D. ④③①②
D 【解析】试题分析:根据直线外一点作已知直线的垂线的方法作BH⊥AC即可. 【解析】 用尺规作图作△ABC边AC上的高BH,作法如下: 取一点K,使K和B在AC的两侧; 以B为圆心,BK长为半径作弧,交直线AC于点D和E; 分别以点D,E为圆心,大于DE的长为半径作弧,两弧交于F; 作射线BF,交边AC于点H; 所以,BH就是所求作的高. 故正确...查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:解答题
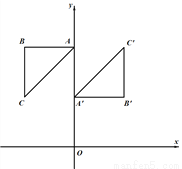
如图,在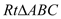 中,
中, ,
, ,
,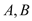 的坐标分别为
的坐标分别为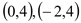 ,将
,将 绕点
绕点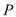 旋转
旋转 后得到
后得到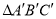 ,其中点
,其中点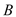 的对应点
的对应点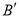 的坐标为
的坐标为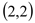 .
.
(1)求出点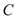 的坐标;
的坐标;
(2)求点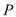 的坐标,并求出点
的坐标,并求出点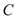 的对应点
的对应点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
(【材料阅读】阅读下列一段文字,然后回答下列问题.
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算:
MN=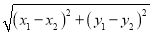 .
.
例如:已知P(3,1)、Q(1,﹣2),则这两点间的距离PQ=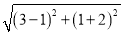 =
=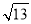 .
.
【直接应用】
(1)已知A(2,-3)、B(-4,5),试求A、B两点间的距离;
(2)已知△ABC的顶点坐标分别为A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
【深度应用】
(3)如图,在平面直角坐标系xOy中,二次函数y=x2﹣4的图象与x轴相交于两点A、B,(点A在点B的左边)
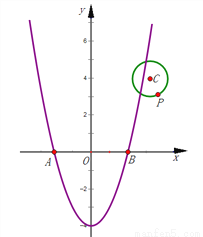
①求点A、B的坐标;
②设点P(m,n)是以点C(3,4)为圆心、1为半径的圆上一动点,求PA2+PB2的最大值;
(1)AB=10; (2)△ABC是直角三角形;(3)①A(-2,0)B(2,0);②80. 【解析】分析:(1)依据两点间的距离公式可求得AB的长;(2)依据两点间的距离公式可求得AB、AC、BC的长,然后依据勾股定理的逆定理可对△ABC的形状作出判断;(3)①令y=0得:x²-4=0,解得x=2或x=-2,故此可得到A,B的坐标;②首先依据两点间的距离公式表示出PA²+PB²的长,通过化...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com