练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知圆柱的高为3 cm,当圆柱的底面半径r(cm)由小变大时,圆柱的体积V(cm3)随之变化,则V与r的关系式是(　　)

    A. V=πr2 B. V=3πr2 C. V=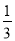πr2 D. V=9πr2

    B 【解析】∵圆柱的体积=底面积×高，该圆柱高为3cm，底面半径为cm，体积为cm3， ∴. 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下2.1.2 垂线的定义与性质 同步练习 题型：解答题

    在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是多少?

    120° 【解析】试题分析：需要分类讨论，C,D在AB同侧，∠AOC+∠COD+∠DOB=180°，易得∠BOD；C,D在AB异侧，∠COA+∠AOD=90°，∠AOD+∠BOD=180°，可得∠BOD. 试题解析： 【解析】 (1)如图，当OC，OD在AB一侧时， ∵OC⊥OD，∴∠COD＝90°. ∵∠AOC＝30°，∴∠BOD＝180°－∠COD－∠AOC＝6...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第一章　整式的乘除 单元测试卷 题型：解答题

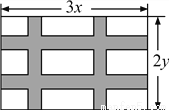
    如图，要设计一幅长为3xcm、宽为2ycm的长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度为bcm，问空白区域的面积是多少？

    6xy－6ax－4by＋4ab(cm2) 【解析】试题分析：此题可将彩条平移到如图所示的长方形的靠边处，则空白部分组成一个长方形，这个大长方形长（3x-2b）cm，宽为（2y-2a），则空白部分的面积=长×宽即可得出． 试题解析： 可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”， 一个大的空白长方形，则该长方形的面积就是空白区域的面积. 而这个...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：解答题

    自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.

    (1)观察图形,填写下表:

    链条的节数/节

    2

    3

    4

    …

    链条的长度/cm

    …

    (2)如果x节链条的长度为y(cm),那么y与x之间的关系式是什么?

    (3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?

    (1)4.2;5.9;7.6(2)即y=1.7x+0.8(3)这辆自行车上的链条(安装后)总长度为102 cm. 【解析】试题分析： （1）根据题意计算即可得到当链条节数为2、3、4时，链条的相应长度，填入表格中即可； （2）由题意可知，第1节链条长度为2.5cm，后面每增加1节链条，长度增加1.7cm，由此即可得到链条长度与链条节数之间的关系式； （3）将代入（2）中所得...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系 同步练习 题型：单选题

    一个长方体的体积为12 cm3,当底面积不变,高增大时,长方体的体积发生变化,若底面积不变,高变为原来的3倍,则体积变为(　　)

    A. 12 cm3 B. 24 cm3 C. 36 cm3 D. 48 cm3

    C 【解析】设长方体的底面积为s，高为h，则其体积v=sh， ∴当长方体的底面积不变，高变为原来的3倍时，其体积也变为原来的3倍， ∴若原来的体积为12cm3，则现在的体积为：36cm3.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

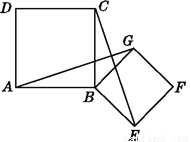
    如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:

    (1)AG=CE;

    (2)AG⊥CE.

    (1)答案见解析;(2)答案见解析 【解析】试题分析：（1）由正方形的性质有AB=CB，∠ABC=∠GBE=90°，BG=BE，进而得出∠ABG=∠CBE，由SAS证明△ABG≌△CBE，得出对应边相等即可； （2）由△ABG≌△CBE，得出对应角相等∠BAG=∠BCE，由∠BAG+∠AMB=90°，对顶角∠AMB=∠CMN，得出∠BCE+∠CMN=90°，证出∠CNM=90°即可． ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型：解答题

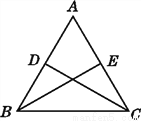
    如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.

    答案见解析 【解析】试题分析：由中点定义及AB=AC，可得到AD=AE，再通过SAS证明△ADC≌△AEB即可． 试题解析：【解析】 △ADC≌△AEB．理由如下： ∵AB=AC，D，E分别是AB，AC的中点，∴AD=AE． 在△ADC和△AEB中，∵AC=AB，∠A=∠A(公共角)，AD=AE， ∴△ADC≌△AEB(SAS)．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型：单选题

    如图，是一台自动测温仪记录的图象，它反映了我市冬季某天气温T随时间t变化而变化的关系，观察图象得到下列信息，其中错误的是（ ）

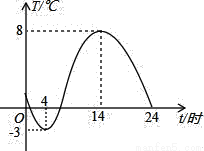
    A. 凌晨4时气温最低为－3℃

    B. 14时气温最高为8℃

    C. 从0时至14时，气温随时间增长而上升

    D. 从14时至24时，气温随时间增长而下降

    C 【解析】试题分析：A．∵由图象可知，在凌晨4点函数图象在最低点﹣3，∴凌晨4时气温最低为﹣3℃，故本选项正确； B．∵由图象可知，在14点函数图象在最高点8，∴14时气温最高为8℃，故本选项正确； C．∵由图象可知，从4时至14时，气温随时间增长而上上升，不是从0点，故本选项错误； D．∵由图象可知，14时至24时，气温随时间增长而下降，故本选项正确． 故选C． ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.1 三角形及其内角和 同步练习 题型：填空题

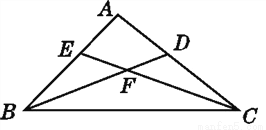
    如图,以CD为公共边的三角形是____________;∠EFB是____________的内角;在△BCE中,BE所对的角是____________,∠CBE所对的边是____________;以∠A为公共角的三角形是____________. 

    △CDF与△BCD △BEF ∠BCE CE △ABD,△ACE和△ABC 【解析】试题分析：以CD为公共边的三角形是△CDF与△BCD；∠EFB是△BEF的内角；在△BCE中，BE所对的角是∠BCE，∠CBE所对的边是CE；以∠A为公共角的三角形是△ABD，△ACE和△ACB． 故答案为：△CDF与△BCD；△BEF；∠BCE；CE；△ABD，△ACE和△ABC．

    查看答案和解析>>

    同步练习册答案