练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    有一张三角形纸片ABC，∠A＝80°，点D是AC边上一点，沿BD方向剪开三角形纸片后，发现所得两张纸片均为等腰三角形，则∠C的度数可以是__________．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：吉林省长春市校2018届九年级下学期第一次模拟考试数学试卷 题型：单选题

    如图，AB是⊙O的直径，点C在⊙O上，P是线段OB上的任意一点．若∠CAB=40°，则∠APC的大小不可能为（ ）

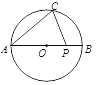
    A. 100° B. 90° C. 50 D. 40°

    查看答案和解析>>

    科目：初中数学 来源：北京市2018年中考数学试卷 题型：解答题

    计算：．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018年中考数学试卷 题型：单选题

    下列几何体中，是圆柱的为

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018年中考模拟试卷（一）数学试卷 题型：解答题

    不用圆规、三角板，只用没有刻度的直尺，用连线的方法在图1、2中分别过圆外一点A作出直径BC所在射线的垂线．

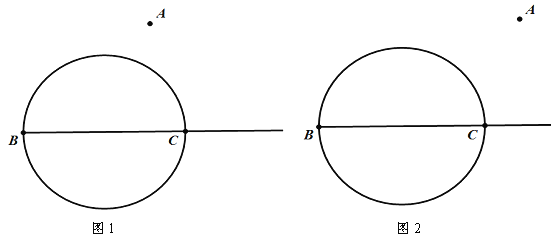
    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018年中考模拟试卷（一）数学试卷 题型：填空题

    分解因式：2x2-8x+8=__________.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（湘教版）期末单元测试卷 第2章 四边形 题型：解答题

    如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF=90°，且EF交正方形外角平分线CF于点F．请你认真阅读下面关于这个图的探究片段，完成所提出的问题．

    （1）探究1：小强看到图（*）后，很快发现AE=EF，这需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（一个是直角三角形，一个是钝角三角形），考虑到点E是边BC的中点，因此可以选取AB的中点M，连接EM后尝试着去证△AEM≌EFC就行了，随即小强写出了如下的证明过程：

    证明：如图1，取AB的中点M，连接EM．

    ∵∠AEF=90°

    ∴∠FEC+∠AEB=90°

    又∵∠EAM+∠AEB=90°

    ∴∠EAM=∠FEC

    ∵点E，M分别为正方形的边BC和AB的中点

    ∴AM=EC

    又可知△BME是等腰直角三角形

    ∴∠AME=135°

    又∵CF是正方形外角的平分线

    ∴∠ECF=135°

    ∴△AEM≌△EFC（ASA）

    ∴AE=EF

    （2）探究2：小强继续探索，如图2，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，发现AE=EF仍然成立，请你证明这一结论．

    （3）探究3：小强进一步还想试试，如图3，若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE=EF是否成立呢？若成立请你完成证明过程给小强看，若不成立请你说明理由．

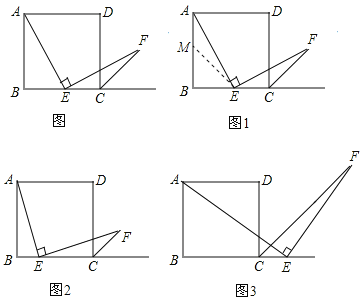
    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学下册（湘教版）期末单元测试卷 第2章 四边形 题型：填空题

    如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为6和8时，则阴影部分的面积为__________．

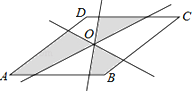
    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级下期末复习第九章不等式与不等式组期末单元复习卷人教版数学试卷 题型：单选题

    若关于x的不等式组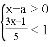无解，则a的取值范围是（　　）

    A. a＞2 B. a≥2 C. 1＜a≤2 D. 1≤a＜2

    查看答案和解析>>

    同步练习册答案