练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.

    30°. 【解析】试题分析：利用三角形的内角和为180°即可得到∠ABC或∠C的度数，进而利用外角可求得∠DAB的度数，从而求得∠ABD的度数． 试题解析：∵∠BAC=4∠ABC=4∠C， ∴∠BAC+∠ABC+∠C=180°， 即∠C=∠ABC=180×=30°， ∴∠DAB=∠C+∠ABC=30°+30°=60°， ∵BD⊥AC， ∴∠BDA=90°，...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：四川省实验学校2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    （10分）为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如下表（注：水费按月份结算，m3表示立方米）：

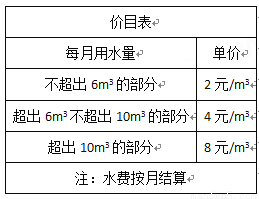
    请根据上表的内容解答下列问题：

    （1）填空：若该户居民2月份用水4m3，则应收水费_____元；

    （2）若该户居民3月份用水am3（其中6m3＜a＜10m3），则应收水费多少元？（用含a的代数式表示，并化简）

    （3）若该户居民4，5两个月共用水15m3，并且4月份用水量不超过6 m3，设4月份用水xm3，求该户居民4，5两个月共交水费多少元？（用含x的代数式表示，并化简）

    （1）8元 ；（2）4a-12；（3）48-2x或68-6x 【解析】试题分析：对于（1），不超过6m3，单价为2元，水费=单价×数量，据此解答； 对于（2），由题意得水费=单价为2元的6m3的水费+单价为4元的超过6m3的水费； 对于（3）应分情况讨论：4月份不超过6m3，5月份10立方米以上；或4月份不超过6m3，5月份在6-10立方米之间. 【解析】 （1）2×4=...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.2 用“内错角、同旁内角”判定平行线 同步练习 题型：单选题

    如图,直线AB,CD被直线EF所截,则∠3的同旁内角是(　　)

    A. ∠1 B. ∠2 C. ∠4 D. ∠5

    B 【解析】试题分析：A、∠3与∠1属于同位角，故本选项正确；B、∠3与∠2属于同旁内角，故本选项错误； C、∠3与∠4于邻补角，故本选项错误；D、∠3与∠5于内错角，故本选项错误． 故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（2）同步练习 题型：单选题

    如图，下列说法正确的是 （ ）

    A. ∠1和∠2是内错角 B. ∠1和∠3是内错角

    C. ∠1和∠4是内错角 D. ∠1和∠5是内错角

    D 【解析】A. ∵∠1和∠2是同旁内角，故不正确； B. ∵∠1和∠3是同位角，故不正确； C. ∵ ∠1和∠4不具备特殊位置关系，故不正确； D. ∵∠1和∠5是内错角，故正确； 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下5.3.2线段垂直平分线练习 题型：单选题

    已知△ABC中，AB=AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是70cm和48cm，则△ABC的腰和底边长分别为（ ）

    A．24cm和22cm B．26cm和18cm

    C．22cm和26cm D．23cm和24cm

    C 【解析】 试题分析：根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出△DBC的周长=AC+BC，再根据两个三角形的周长求出AB，然后BC的值即可． 【解析】 ∵AB的垂直平分线交AC于D， ∴AD=BD， ∴△DBC的周长=BD+CD+BC=AD+CD+BC=AC+BC， ∵△ABC和△DBC的周长分别是70cm和48cm， ∴...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.5 利用三角形全等测距离 同步练习 题型：解答题

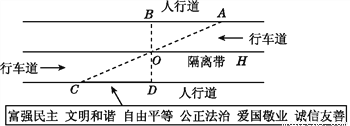
    杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下:

    如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.

    20米. 【解析】试题分析：已知AB∥CD，根据平行线的性质可得∠ABO=∠CDO，再由垂直的定义可得∠CDO=90°，可得OB⊥AB，根据相邻两平行线间的距离相等可得OD=OB，即可根据ASA定理判定△ABO≌△CDO，由全等三角形的性质即可得CD=AB=20m． 试题解析：∵AB∥CD，∴∠ABO=∠CDO， ∵OD⊥CD，∴∠CDO=90°， ∴∠ABO=90°，即O...

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册第四章三角形4.3探索三角形全等的条件 同步练习 题型：解答题

    已知：如图，AB=AD，BC=DE，AC=AE，BC交DE于点M、交AD于点N。求证：∠ 1 = ∠ 2 = ∠3。

    证明见解析 【解析】试题分析：由边边边证得△ABC≌△ADE，由全等三角形的性质得出∠BAC=∠DAE， ∠B=∠D，进而∠1=∠2，再由三角形内角和定理及等量代换即可得证. 在△ABC和△DCB中， ∴△ABC≌△ADE(SSS)， ∴∠BAC=∠DAE， ∠B=∠D， 即∠ 1+∠ DAC=∠ 2+∠ DAC， ∴∠1=∠2， ∵ ∠ 3+∠ DNM+...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.2 图形的全等 同步练习 题型：解答题

    如图,已知△ABC≌△EDC,指出其对应边和对应角.

    见解析 【解析】试题分析：利用全等三角形的性质分别得出对应点进而得出对应边与对应角关系． 试题解析：△ABC≌△EDC， ∴AB的对应边是ED，AC的对应边是EC，BC的对应边是DC， ∠A的对应角是∠E，∠B的对应角是∠D，∠ACB的对应角是∠ECD.

    查看答案和解析>>

    科目：初中数学 来源：2017年北师大版七年级数学下册第一章《整式的运算》复习测试卷一 题型：填空题

    ________．

    6 【解析】根据零指数幂的性质和负整指数幂性质、绝对值，可得=1×4+2=6. 故答案为：6.

    查看答案和解析>>

    同步练习册答案