
2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
A. 3×106 B. 3×105 C. 0.3×106 D. 30×104
B 【解析】【解析】 将300000用科学记数法表示为:3×105 .故选B. 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:湖北省襄阳市襄城区2017-2018学年度上学期期中考试七年级数学试卷 题型:解答题
已知:多项式 2x2+my-12与多项式nx2-3y+6的差与x,y的大小无关.
求:m+n+mn的值.
-7 【解析】试题分析:根据题意,可将此题化为关于Ax2+By+C=0的形式,因为不含有x、y,即x、y的系数为0,从而求出m和n,代入求解即可. 试题解析:【解析】 (2x2+my﹣12)﹣(nx2﹣3y+6)=(2﹣n)x2+(m+3)y﹣18,因为差中不含有x、y,所以2﹣n=0,m+3=0,所以n=2,m=﹣3,故m+n+mn=﹣3+2+(﹣3)×2=﹣7.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:单选题
等腰三角形的一个内角是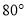 ,则它顶角的度数是( ).
,则它顶角的度数是( ).
A. 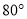 B.
B. 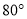 或
或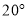 C.
C. 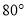 或
或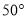 D.
D. 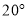
查看答案和解析>>
科目:初中数学 来源:内蒙古2017年中考数学二模试卷 题型:填空题
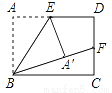
如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=________.
查看答案和解析>>
科目:初中数学 来源:内蒙古2017年中考数学二模试卷 题型:单选题
若ab<0,则正比例函数y=ax与反比例函数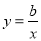 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
A. 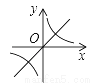 B.
B. 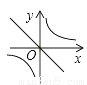
C. 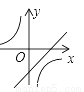 D.
D. 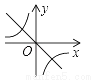
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古中考数学二模试卷 题型:解答题
如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
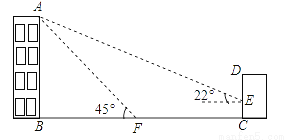
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈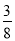 ,cos22°≈
,cos22°≈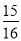 ,tan22°≈
,tan22°≈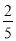 )
)
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古中考数学二模试卷 题型:填空题
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论是________.
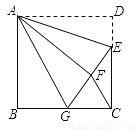
查看答案和解析>>
科目:初中数学 来源:内蒙古2018届九年级(上)期中数学试卷 题型:解答题
某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)设计费能达到24000元吗?为什么?
(3)当x是多少米时,设计费最多?最多是多少元?
(1)S=﹣x2+8x,其中0<x<8;(2)能,理由见解析;(3)当x=4米时,矩形的最大面积为16平方米,设计费最多,最多是32000元. 【解析】试题分析:(1)由矩形的一边长为x、周长为16得出另一边长为8﹣x,根据矩形的面积公式可得答案; (2)由设计费为24000元得出矩形面积为12平方米,据此列出方程,解之求得x的值,从而得出答案; (3)将函数解析式配方成顶点式,...查看答案和解析>>
科目:初中数学 来源:江苏省盐城市阜宁县2018届九年级上学期期末考试数学试卷 题型:填空题
若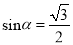 ,则锐角
,则锐角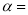 ____
____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com