
已知二次函数y=x2+2x﹣3,当自变量x取m时,对应的函数值小于0,设自变量分别取m﹣4,m+4时对应的函数值为y1,y2,则下列判断正确的是( )
A. y1<0,y2<0 B. y1<0,y2>0 C. y1>0,y2<0 D. y1>0,y2>0
D 【解析】试题分析:令y=0,则x2+2x﹣3=0,解得x=1或x=3,其对称轴为x=2,则1<m<3时,y<0,因此m-4与m+4时对应的y1>0,y2>0. 故选:D科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
分式方程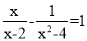 的解是( )
的解是( )
A. ﹣ B. ﹣2 C. ﹣
B. ﹣2 C. ﹣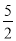 D.
D. 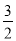
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:填空题
把抛物线y=x2-4x+5的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是
y=x2-10x+24. 【解析】 试题分析:先利用配方法将抛物线y=x2-4x+5写成顶点式,再根据“上加下减,左加右减”的原则进行解答即可. 试题解析:y=x2-4x+5=(x-2)2+1, 由“左加右减”的原则可知,抛物线y=(x-2)2+1的图象向右平移3个单位所得函数图象的关系式是:y=(x-5)2+1; 由“上加下减”的原则可知,抛物线y=(x-5)2+1的图...查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
【发现证明】
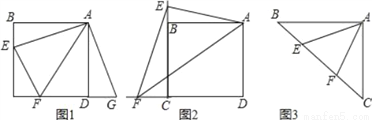
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:填空题
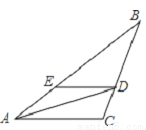
如图,在△ABC中,AD平分∠BAC,与BC边的交点为D,且DC= BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为__________.
BC,DE∥AC,与AB边的交点为E,若DE=4,则BE的长为__________.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
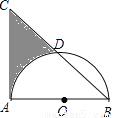
A. 24-4π B. 32-4π C. 32-8π D. 16
A 【解析】试题分析:连接AD,OD, ∵等腰直角△ABC中, ∴∠ABD=45°. ∵AB是圆的直径, ∴∠ADB=90°, ∴△ABD也是等腰直角三角形, ∴. ∵AB=8, ∴AD=BD=4, ∴S阴影=S△ABC-S△ABD-S弓形AD=S△ABC-S△ABD-(S扇形AOD-S△ABD) =×8×8-×4×4-+××4×4...查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
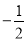 的倒数是( )
的倒数是( )
A. 2 B. ﹣2 C. 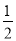 D.
D. 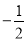
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
已知x+y=1,xy=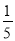 ,求下面各式的值:
,求下面各式的值:
(1)x2y+xy2;
(2)(x2+1)(y2+1).
(1) ;(2) 【解析】试题分析:(1)原式提取公因式后,将各自的值代入计算即可求出值;(2)原式利用多项式乘以多项式法则计算,再利用完全平方公式变形后,将各自的值代入计算即可求出值; 试题解析(1)∵x+y=1,xy=, ∴原式=xy(x+y)= ; (2)∵x+y=1,xy=, ∴原式= x2 y2+ x2+ y2+1= x2 y2+(x+y)2?2xy+1=+...查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:解答题
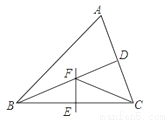
如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.
(1)若∠A=60°,∠ABD=24°,求∠ACF的度数;
(2)若EF=4,BF:FD=5:3,S△BCF=10,求点D到AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com