
某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
(1)平均数为320件,中位数是210件,众数是210件;(2)不合理,定210件 【解析】试题分析:(1)根据平均数、中位数和众数的定义即可求得结果; (2)把月销售额320件与大部分员工的工资比较即可判断. (1)平均数件, ∵最中间的数据为210, ∴这组数据的中位数为210件, ∵210是这组数据中出现次数最多的数据, ∴众数为210件; (... 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:填空题
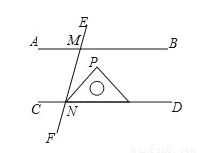
如图,AB∥CD,直线EF分别交AB、CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于_____度.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2=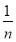 [(x1-
[(x1-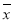 )2+(x2-
)2+(x2-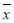 )2++(xn-
)2++(xn-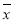 )2]
)2]
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
对于一元二次方程ax2+bx+c=0 (a≠0),下列说法中错误的是( )
A. 当a>0,c<0时,方程一定有实数根
B. 当c=0时,方程至少有一个根为0
C. 当a>0,b=0,c<0时,方程的两根一定互为相反数
D. 当abc<0时,方程的两个根同号,当abc>0时,方程的两个根异号
D 【解析】解:A.正确.当a>0,c<0时,△=b2﹣4ac>0,则方程一定有实数根; B.正确.当c=0时,则ax2+bx=0,则方程至少有一个根为0; C.正确.当a>0,b=0,c<0时,方程两根为x1,x2,x1+x2==0,则方程的两根一定互为相反数; D.错误.当ac<0时,方程的两个根异号,当ac>0时,方程的两个根同号. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
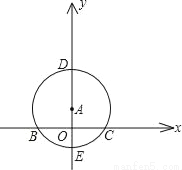
已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,﹣1)
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连接PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:填空题
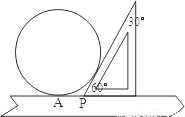
为了测量一个圆铁环的半径,某同学用了如下方法,将铁环平放在水平桌面上,用有一个角为30°的直角三角板和刻度尺按如图所示的方法得到相关数据,进而求出铁环半径,若测得PA=5cm,则铁环的半径是_____cm.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:单选题
我们知道,溶液的酸碱度由PH确定.当PH>7时,溶液呈碱性;当PH<7时,溶液呈酸性.若将给定的HCl溶液加水稀释,那么在下列图象中,能反映HCl溶液的PH与所加水的体积(V)的变化关系的是( )
A. 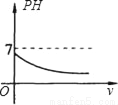 B.
B. 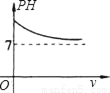 C.
C. 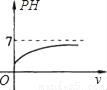 D.
D. 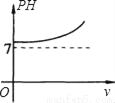
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA.
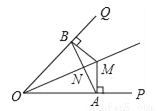
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型:单选题
甲、乙两个同学分别解一道二次项系数是1的一元二次方程,甲因把一次项系数看错了,而解得方程两根为﹣3和5,乙把常数项看错了,解得两根为2和2,则原方程是....( )
A. x2+4x﹣15=0 B. x2﹣4x﹣15=0 C. x2+4x+15=0 D. x2﹣4x+15=0
B 【解析】甲的常数项是对的,所以常数项为: -3×5 = -15, 乙的一次项系数是对的,所以是一次项系数为:-(2+2)= -4, 原方程是 x2 - 4 x -15 = 0, 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com