练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

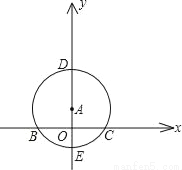
    已知：如图，点A在y轴上，⊙A与x轴交于B、C两点，与y轴交于点D（0，3）和点E（0，﹣1）

    （1）求经过B、E、C三点的二次函数的解析式；

    （2）若经过第一、二、三象限的一动直线切⊙A于点P（s，t），与x轴交于点M，连接PA并延长与⊙A交于点Q，设Q点的纵坐标为y，求y关于t的函数关系式，并观察图形写出自变量t的取值范围；

    （3）在（2）的条件下，当y=0时，求切线PM的解析式，并借助函数图象，求出（1）中抛物线在切线PM下方的点的横坐标x的取值范围．

    （1）y=x2﹣1（2）y=﹣t+2（1＜t＜3）（3）＜x＜ 【解析】试题分析：（1）已知点D（0，3）和点E（0，-1），可以得到圆的直径，连接AC，根据垂径定理，以及勾股定理就可以求出OB，OE，OC的长度，得到三点的坐标，根据待定系数法就可以求出二次函数的解析式． （2）过点P作PF⊥y轴于F，过点Q作QN⊥y轴于N，易证△PFA≌△QNA，则FA=NA，即|t-1|=|1-y...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型：解答题

    计算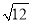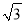： +|﹣3|﹣2sin60°﹣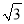（）2+20160．

    1 【解析】试题分析：先分别对根式、绝对值、三角函数、乘方进行运算，再进行加减运算. 试题解析：原式=2+3－-2×－3+1=2+3－－－3+1=1.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型：单选题

    以下图标是轴对称图形的是( )

    A. B. C. D.

    D 【解析】A不是轴对称图形，故不符合题意；B不是轴对称图形，故不符合题意；C不是轴对称图形，故不符合题意；D是轴对称图形，故符合题意， 故选D.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：填空题

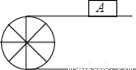
    如图半径为30cm的转动轮转过80°时，传送带上的物体A平移的距离为_____．

    【解析】【解析】 由题意得，R=30cm，n=80°，故l= = （cm）． 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级（上）期中数学试卷 题型：单选题

    如图，圆锥的底面半径OB=6cm，高OC=8cm．则这个圆锥的侧面积是（ ）

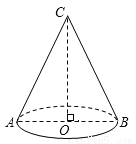
    A. 30cm2 B. 30πcm2 C. 60πcm2 D. 120cm2

    C 【解析】试题分析：先利用勾股定理计算出圆锥的母线长=，然后利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式计算这个圆锥漏斗的侧面积=•2π•6•10=60π（cm2）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省扬州市中考数学模拟试卷（二） 题型：解答题

    某公司销售部有营销人员15人，销售部为了制定某种商品的月销售定额，统计了这15人某月的销售如下:

    每人销售件数
     

    1800
     

    510
     

    250
     

    210
     

    150
     

    120
     

    人数
     

    1
     

    1
     

    3
     

    5
     

    3
     

    2
     

    （1）求这15位营销人员该月销售量的平均数、中位数和众数.

    （2）假设销售部负责人把每位营销员的月销售额定为320件，你认为是否合理?为什么?如不合理，请你制定一个合理的销售定额，并说明理由.

    （1）平均数为320件，中位数是210件，众数是210件；（2）不合理，定210件 【解析】试题分析：（1）根据平均数、中位数和众数的定义即可求得结果； （2）把月销售额320件与大部分员工的工资比较即可判断. （1）平均数件， ∵最中间的数据为210， ∴这组数据的中位数为210件， ∵210是这组数据中出现次数最多的数据， ∴众数为210件； （...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省扬州市中考数学模拟试卷（二） 题型：填空题

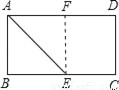
    如图所示，一张矩形纸片，要折叠出一个最大的正方形，小明把矩形上的一个角沿折痕AE翻折上去，使AB与AD边上的AF重合，则四边形ABEF就是一个大的正方形，他判定的方法是_____．

    有一组邻边相等的矩形是正方形 【解析】根据翻折变换及正方形的判定方法进行分析即可得其判定方法是：有一组邻边相等的矩形是正方形． 故答案为：有一组邻边相等的矩形是正方形.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省中考数学模拟试卷 题型：解答题

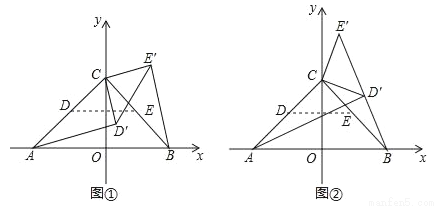
    在平面直角坐标系中，点 A（﹣2，0），B（2，0），C（0，2），点 D，点E分别是 AC，BC的中点，将△CDE绕点C逆时针旋转得到△CD′E′，及旋转角为α，连接 AD′，BE′．

    （1）如图①，若 0°＜α＜90°，当 AD′∥CE′时，求α的大小；

    （2）如图②，若 90°＜α＜180°，当点 D′落在线段 BE′上时，求 sin∠CBE′的值；

    （3）若直线AD′与直线BE′相交于点P，求点P的横坐标m的取值范围（直接写出结果即可）．

    （1）60°；（2）；（3）﹣≤m≤． 【解析】试题分析：(1)如图1中，根据平行线的性质可得∠AD′C=∠E′CD′=90°，再根据AC=2CD′，推出∠CAD′=30°，由此即可解决问题； (2)如图2中，作CK⊥BE′于K．根据勾股定理和等腰直角三角形的性质求出CK的长，再根据sin∠CBE′= ，即可解决问题；(3)根据图3、图4分别求出点P横坐标的最大值以及最小值即可解决问题. ...

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型：解答题

    用适当的方法解方程：

    （1）2x2﹣4x﹣1=0 （2）（x+1）2=6x+6． （3）2x2﹣7x+3=0

    （1）x1=1+，x2=1﹣；（2）x1=﹣1，x2=5；（3）x1=，x2=3. 【解析】试题分析：（1）利用配方法进行求解即可； （2）变形后利用因式分解法进行求解即可； （3）利用公式法进行求解即可. 试题解析：（1）x2﹣2x=， x2﹣2x+1=， （x﹣1）2=， x﹣1=， 所以x1=1+，x2=1﹣； （2）（x+1）2﹣6（x...

    查看答案和解析>>

    同步练习册答案