
在抛物线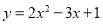 上的点是( ).
上的点是( ).
A. 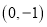 B.
B. 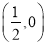 C.
C. 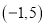 D.
D. 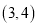
科目:初中数学 来源:北京101中学2017-2018学年上学期初中七年级期末考试数学试卷 题型:解答题
计算:
(1)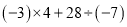 . (2)
. (2)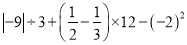 .
.
查看答案和解析>>
科目:初中数学 来源:陕西省西安市师大2017-2018学年初三期中考试数学试卷 题型:单选题
某人沿着倾斜角为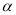 的斜坡前进了
的斜坡前进了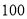 米,则他上升的高度是( ).
米,则他上升的高度是( ).
A. 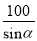 米 B.
米 B. 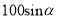 C.
C. 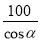 D.
D. 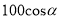 米
米
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:填空题
在平面直角坐标系中, 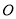 为原点,
为原点, 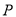 点的坐标为
点的坐标为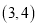 ,
, 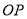 与
与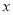 轴的夹角为
轴的夹角为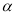 ,则
,则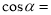 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:陕西省2018届九年级上学期期中考试数学试卷 题型:单选题
在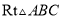 中,
中, 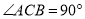 ,
, 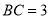 ,
, 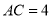 ,
, 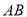 的垂直平分线
的垂直平分线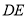 交
交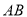 于点
于点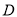 ,交
,交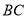 的延长线于点
的延长线于点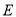 ,则
,则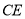 的长为( ).
的长为( ).
A. 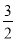 B.
B. 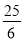 C.
C. 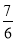 D.
D. 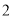
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
考古学家从幼发拉底河附近的一座寺庙里,发掘出数千块泥板书,他们从泥板书中发现美索不达米亚的祭祀已经知道平方表的用法,并能够利用平方表算出任意两个自然数的乘积.
例如:计算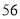 乘以
乘以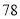 ,祭祀们会按下面的流程操作:
,祭祀们会按下面的流程操作:
第一步: 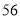 加上
加上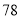 ,将和除以
,将和除以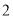 得
得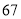 ;
;
第二步: 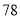 减去
减去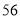 ,将差除以
,将差除以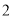 得
得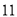 ;
;
第三步:查平方表,得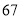 的平方是
的平方是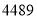 ;
;
第四步:查平方表,得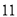 的平方是
的平方是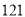 ;
;
第五步: 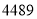 减去
减去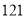 ,得到答案
,得到答案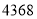 .
.
于是他们便得出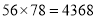 .
.
请你利用所学的代数知识,设两个自然数分别为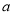 、
、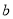 ,对泥板书计算两个自然数乘积的合理性做出解释.
,对泥板书计算两个自然数乘积的合理性做出解释.
查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
多项式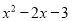 与
与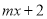 的乘积化简后
的乘积化简后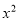 项的系数是
项的系数是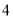 ,则
,则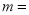 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州萧山区高桥中学2017-2018学年七年级上学期期中数学试卷 题型:解答题
大家知道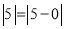 ,它在数轴上的意义是表示
,它在数轴上的意义是表示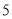 的点与原点(即表示
的点与原点(即表示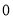 的点)之间的距离,又如式子
的点)之间的距离,又如式子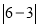 ,它在数轴上的意义是表示
,它在数轴上的意义是表示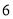 的点与表示
的点与表示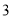 的点之间的距离.
的点之间的距离.
(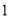 )在数轴上的意义是表示
)在数轴上的意义是表示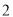 的点与表示
的点与表示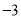 的点之间的距离是__________.
的点之间的距离是__________.
(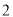 )反过来,式子
)反过来,式子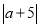 在数轴上的意义是__________.
在数轴上的意义是__________.
(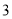 )试用数轴探究:当
)试用数轴探究:当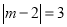 时,
时, 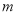 的值为__________.
的值为__________.
(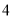 )进一步探究:
)进一步探究: 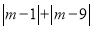 的最小值为__________.
的最小值为__________.
(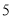 )最后发现:当
)最后发现:当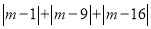 的值最小时,
的值最小时, 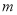 的值为__________.
的值为__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 第11章 三角形 单元测试卷 题型:填空题
如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=76°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com