
要调查某校学生周日的睡眠时间,下列选项调查对象中最合适的是( )
A. 选取一个班级的学生
B. 选取50名男生
C. 选取50名女生
D. 在该校各年级中随机选取50名学生
D 【解析】随机抽样是最简单和最基本的抽样方法,抽样时要注意样本的代表性和广泛性,选取该校一个班级的学生、选取该校50名男生、选取该校50名男生,这些对象都缺乏代表性和广泛性,得到的结果也缺乏准确性, 故选D. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年秋四川泸县第四中学九年级第二次阶段性考试数学试卷 题型:单选题
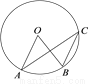
如图2,点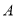 、
、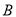 、
、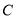 在⊙O上,
在⊙O上, 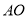 ∥
∥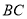 ,
, 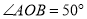 ,则
,则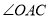 的度数是
的度数是
A. 25° B. 30° C. 35° D. 40°
A 【解析】∵AO ∥ BC,∴∠OAC=∠ACB, 又∠AOB与∠ACB都是弧AB所对的角, ∴∠ACB= ∠AOB=×50°=25°, ∴∠OAC的度数是25°, 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)练习 题型:单选题
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
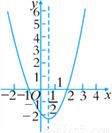
A. 函数有最小值 B. 对称轴是直线x=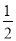
C. 当x<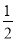 时,y随x的增大而减小 D. 当-1<x<2时,y>0
时,y随x的增大而减小 D. 当-1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期6.1数据的收集 同步练习 题型:填空题
进行数据的收集调查时,在明确调查问题、确定调查对象后,还要完成以下4个步骤:①展开调查 ②得出结论 ③记录结果 ④选择调查方法,但它们的顺序弄乱了,正确的顺序应该是_____(填写序号即可).
④①③②. 【解析】进行数据的调查收集,一般可分为以下4个步骤:④选择调查方法;①展开调查;③记录结果;②得出结论, 故答案为:④①③②.查看答案和解析>>
科目:初中数学 来源:初一数学第一学期6.1数据的收集 同步练习 题型:单选题
PM2.5指数是测控空气污染程度的一个重要指数.在一年中最可靠的一种观测方法是( )
A. 随机选择5天进行观测
B. 选择某个月进行连续观测
C. 选择在春节7天期间连续观测
D. 每个月都随机选中5天进行观测
D 【解析】A、选项样本容量不够大,5天太少,故选项错误;B、选项的时间没有代表性,集中一个月没有普遍性,故选项错误;C、选项的时间没有代表性,集中春节7天没有普遍性选项一年四季各随机选中一个星期也是样本容量不够大,故选项错误;D、样本正好合适,故选项正确, 故选D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型:解答题
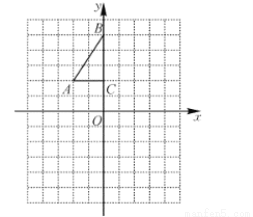
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(1)测试 题型:解答题
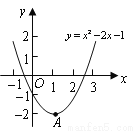
如图,已知二次函数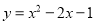 的图象的顶点为A.二次函数
的图象的顶点为A.二次函数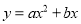 的图象与x轴交于原点O及另一点C,它的顶点B在函数
的图象与x轴交于原点O及另一点C,它的顶点B在函数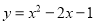 的图象的对称轴上.
的图象的对称轴上.
(1)求点A与点C的坐标;
(2)当四边形AOBC为菱形时,求函数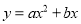 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点, 将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是 ( )
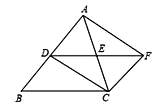
A. 矩形 B. 菱形 C. 正方形 D. 梯形
A 【解析】试题分析:根据旋转得到AD=CF,AD∥CF,则四边形ADCF为平行四边形,根据AC=BC,D为中点则∠ADC=90°,则四边形ADCF为矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com