
一个袋子中装有3个红球和2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下,随机从袋中摸出2个球,其中2个球颜色不相同的概率是
A. 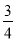 B.
B. 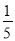 C.
C. 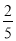 D.
D. 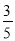
科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型:解答题
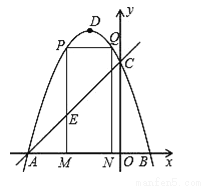
如图,抛物线y=﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM.如图,点P在点Q左边,试用含m的式子表示矩形PQNM的周长;
(3)当矩形PQNM的周长最大时,m的值是多少?并求出此时的△AEM的面积;
(4)在(3)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=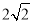 DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:填空题
若关于x的一元二次方程x2 -4x +m = 0有两个相等的实数根,则m =______.
4 【解析】∵一元二次方程x2 -4x +m = 0有两个相等的实数根, ∴△=(-4)2-4m=0, ∴4m=16, ∴m=4.查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:解答题
解下列方程.
(1).(x+3)2=2(x+3)
(2).3x(x-1)=2-2x
(1);(2). 【解析】试题分析:(1)(2)因式分解法解方程. 试题解析: (1).(x+3)2=2(x+3) (x+3)2-2(x+3)=0, (x+3)(x+3-2)=0, (x+3)(x+1)=0. . (2).3x(x-1)=2-2x 3x(x-1)=2(1-x), 3x(x-1)-2(x-1)=0, (x-1)( 3x...查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:单选题
独山县开展关于精准扶贫、精准扶贫的决策部署以来,某贫困户2014年人均纯收入为2620元,经过帮扶到2016年人均纯收入为3850元,设该贫困户每年纯收入的平均增长率为x,则下面列出的方程中正确的是( )
A. 2620(1+x)2=3850 B. 2620(1+x)=3850
C. 2620(1+2x)=3850 D. 2620(1+x)2=3850
A 【解析】由题意得2620(1+x)2=3850.故选A.查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:解答题
商场购进一种单价为40元的书包,如果以单价50元出售,那么每月可售出30个,根据销售经验,售价每提高5元,销售量相应减少1个.
(1)请写出销售单价提高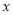 元与总的销售利润y元之间的函数关系式;
元与总的销售利润y元之间的函数关系式;
(2)如果你是经理,为使每月的销售利润最大,那么你确定这种书包的单价为多少元?此时,最大利润是多少元?
(1)x与y的函数关系式为:y=(50+x-40)(30-)(0≤ x ≤150);(2)当这种书包的单价为120元时,每月的销售利润最大为1280元; 【解析】(1)当销售单价提高x元时,销售量减少了个, 此时单价为(50+x)元,销售量为(30-)个 则x与y的函数关系式为:y=(50+x-40)(30-)(0≤ x ≤150) (2)将(1)中函数整理后,得: ...查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型:填空题
如图,已知圆锥的高为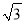 ,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
,高所在直线与母线的夹角为30°,圆锥的侧面积为_____.
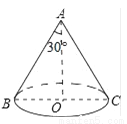
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:解答题
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.
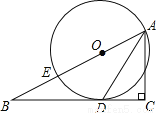
查看答案和解析>>
科目:初中数学 来源:湖北省元月联合测试数学试卷 题型:单选题
将抛物线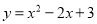 向左平移2个单位,再向上平移1个单位,得到的抛物线的解析式为( )
向左平移2个单位,再向上平移1个单位,得到的抛物线的解析式为( )
A. 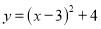 B.
B. 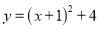 C.
C. 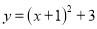 D.
D. 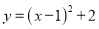
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com