
若关于x的一元二次方程x2 -4x +m = 0有两个相等的实数根,则m =______.
4 【解析】∵一元二次方程x2 -4x +m = 0有两个相等的实数根, ∴△=(-4)2-4m=0, ∴4m=16, ∴m=4.科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:单选题
下列性质中,矩形具有而菱形不一定具有的是( )
A. 对角线相等 B. 对角线互相平分
C. 对角线互相垂直 D. 邻边相等
A 【解析】菱形的性质有:四边形相等,两组对边分别平行,对角相等,邻角互补,对角线互相垂直且平分,且每一组对角线平分一组对角; 矩形的性质有:两组对边分别相等,两组对边分别平行,四个内角都是直角,对角线相等且平分; ∴矩形具有而菱形不一定具有的性质是对角线相等, 故选A.查看答案和解析>>
科目:初中数学 来源:江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型:填空题
用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为______cm.
1. 【解析】试题分析:利用圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长,可设此圆锥的底面半径为r,由题意,得2πr=,解得r=1cm.查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:解答题
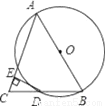
如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:填空题
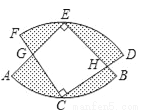
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是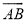 的中点,若扇形的半径为2,则图中阴影部分的面积等于______.
的中点,若扇形的半径为2,则图中阴影部分的面积等于______.
查看答案和解析>>
科目:初中数学 来源:江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型:单选题
已知t是方程x2-2x-1=0的一个根,则代数式2t2-4t的值等于( )
A. 1 B. 2 C. 3 D. 4
B 【解析】∵t是方程x2-2x-1=0的一个根, ∴t2-2t-1=0, ∴t2-2t=1, ∴2t2-4t=2(t2-2t)=2×1=2. 故选B.查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:解答题
某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
(1)y=60+10x, 【解析】试题分析:(1)根据价格每降低1元,平均每天多销售10箱,由每箱降价x元,多卖10x,据此可以列出函数关系式;(2)由利润=(售价﹣成本)×销售量列出函数关系式,求出最大值. 试题解析:(1)根据题意,得:y=60+10x,由36﹣x≥24得x≤12, ∴1≤x≤12,且x为整数; (2)设所获利润为W, 则W=(36﹣x﹣24)(1...查看答案和解析>>
科目:初中数学 来源:河南省2018届九年级上学期期末考试数学试卷 题型:单选题
一个袋子中装有3个红球和2个黄球,这些球的形状、大小、质地完全相同,在看不到球的条件下,随机从袋中摸出2个球,其中2个球颜色不相同的概率是
A. 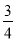 B.
B. 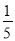 C.
C. 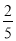 D.
D. 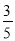
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2018届九年级上学期八校联考数学试卷 题型:单选题
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③25a-5b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
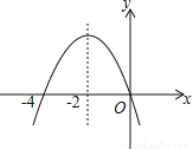
A. 2个 B. 3个
C. 4个 D. 5个
B 【解析】∵抛物线开口向下, ∴a<0, ∵, ∴b=4a,ab>0, ∴①错误,④正确, ∵抛物线与x轴交于﹣4,0处两点, ∴b2﹣4ac>0,方程ax2+bx=0的两个根为x1=0,x2=﹣4, ∴②⑤正确, ∵当a=﹣5时y<0,即...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com